統計学の予期せぬ効用

　小生はこれまで統計学を中心に据えた応用的研究に携わってきた．私のことを知る人達は，数理統計学が小生の趣味だとか性にあっているからだと評して小生の無軌道な便利屋ぶりを揶揄をするのだが，当の本人からすれば，この評は半分もあたっていない．

　本当の理由は，金がなくてもやれるからという悲しい現実に負っているのである．「統計（数理科学）の研究には金がかからない．やる気さえあれば，たとえ収容所の中でもできる．」という説は，私に関する限り，的を射た格言といえよう．

　統計は数学全体からすれば応用数学のそれもほんのさしみのツマ程度のものにすぎない．とはいえ，いざ論文を投稿する段になると，統計に関する知識なしに済ますことは難しいだろう．しかし，論文に必要とされるのはｐ値だけであって，統計＝ｐ値を求めることと勘違いしている人も多いのではなかろうか？

　そのような誤解を払拭するために，また，統計学を応用数学の一部門の水準まで高めるため，統計学の応用領域を拡大創建するために，今回のコラムでは，私がここ数年やってきたことを臆面もなく紹介することにした．

　統計学にはいまだ未完成の部分も多いのであるが，その適用範囲の広さには測り知れないものがあるのである．ご笑読頂ければ幸いである．

　サンゴ礁はサンゴ虫と藻類の共生生態系である．すなわち，動物でありながら，生態系の中では植物的な役割を果たしている．また，聞くところによると，Gattusoを中心とするフランスの海洋研究所では，サンゴ礁は大気中のＣＯ2を下げるのに何の役にも立っていないというデータを出していたらしい．調べたわけではないので誤解があるかもしれないのだが，この研究所は有名なクストーのいたところであって，世界一の海洋研究所といってよいだろう．

　ところが，東大・地球惑星科学の茅根研究室ではまったく正反対の結論に至っていた．ＣＯ2を下げるのに大いに貢献しているというのである．そうでないとサンゴ礁の豊かな生態系を養うことができないわけで，辻褄が合わないというのがその根拠である．

　名門という点では東大だって負けてはいない．油壷に東大の臨界試験場があったと思うが，田崎先生とか団先生の名前は門外漢である私だって知っているくらいである．そこで，間違いを犯しているのはどっちかということが問題になっていたのだが，お互いに相手の間違いを指摘することができず，結論はもちこし状態にあったという．

　炭酸ガスは，太古の地球では大気中に９８％とか９９％という量を占めていたが，植物が繁茂するようになって０．０３％まで減少した．それが石炭，石油を燃やすようになってあと７０年で化石燃料は枯渇するといわれるところまできている．

　大気中の炭酸ガスが急激に増えているという話はご存知と思われるが，現在の増加速度を外挿していくと，２００年後くらいにＣＯ2濃度が４％，すなわち動物の致死量に達するという試算がある．

　つまり，このままだと人類はあと２００年で窒息死ということになる．多少の推定誤差はあるにしても，異常事態であることは明白で，一刻も早く炭酸ガスの上昇を食い止めないと人類は窒息死してしまう．地球温暖化による海面レベルの上昇などと寝ぼけたことをいっている場合ではない．私にいわせれば，これは地球温暖化問題ではなく，人類窒息死問題なのである．

　一刻も早く炭酸ガスの上昇を食い止めないと危ない深刻な状況にあることは確かであるが，こんな簡単なことの認識を拒み，あくまで自国の経済発展を優先させようと画策するのは米中だけである．

　このような背景があるので，サンゴ礁が大気中のＣＯ2を下げるのに寄与しているかどうかが問題となるには自然な成り行きであろう．以下，炭素固定という用語が出てくるが，

　フランスの海洋研究所の試算法によると，サンゴ礁の炭素固定量は７±１８でその信頼区間に０を含んでいる．したがって，サンゴ礁が大気中のＣＯ2を下げるのに役立っているとはいえないわけである．

　一方，東大では，炭素固定量＝３６という値を出していた．しかし，これだけでは炭素固定の出納収支を論ずることはできない．なぜなら，生物データでは誤差がつきものであって，誤差を求めないと何もいえないのである．そんな折り，当時，東大の秦浩司先生（現・ハザマ技術研究所）から誤差見積りの相談を持ちかけられた．３６±？の±？を求めよというものである．

　調べてみると，フランス学派の行った誤差の見積りは，モンテカルロ法によるものであった．モンテカルロ法とは乱数を用いるもので，１００回やれば１００回とも違う答えが出てくる精度が低い方法である．元来，見積り計算の精度が低く，なおかつ計算間違いもあったのであるが，それが巧妙(?)な間違いだったため，だれも計算のウソを見破れなかったのである．

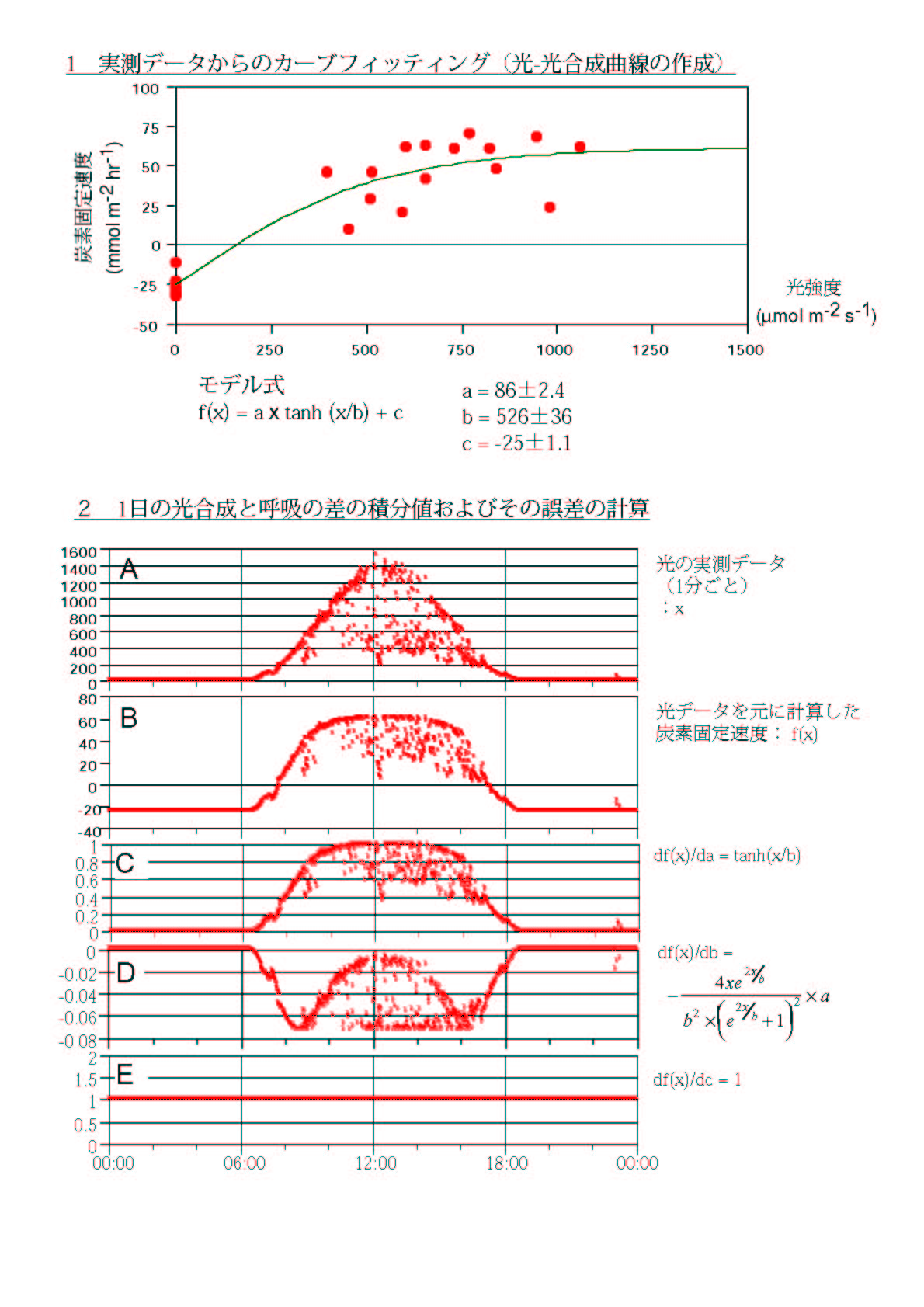
　それに対して，私の考案した方法は誤差論を用いるものである．誤差伝播の法則について，コラム「サンゴ礁と豊饒の海」を参照していただきたいのだが，図にはその際に用いられた実測データと誤差の見積もりのための補助計算を掲げている．

　炭素固定曲線に日照データをかけると，ある程度の光の強さで光合成は頭打ちになるので，台形型のカーブが得られる．そして，夜間は呼吸によってＣＯ2を排出するが，日中は光合成によって大気中のＣＯ2を減らしている．０以上の部分と０以下の部分を相殺して，炭素固定量を計算するのである．

と計算され，炭素固定量はほぼ確実にプラスと判定できた．さらに炭素固定は東大学派，フランス学派いずれのデータを用いても正となることが判明した．この式によって，サンゴ礁は大気中のＣＯ2削減に大きく寄与していることが証明されたことになる．

　このことを受けて，昨年，東大・茅根研究室ではサンゴ礁や地球惑星環境に関する国際シンポジウムを主催した．私は秘かにこの国際シンポことを「Gattusoをガツンといわせる会」を呼んでいたのだが，Gattusoは多忙と現在サンゴ礁の研究から離れていることを理由にシンポシウムへの招待を断ってきたとのことであった．

　学会場では表向きディスカッションを装いながら，お互い相手の意見を聞こうとする気持ちはさらさらなく，単なるディベートと化しているシーンをよく見かけるが，これは非科学的態度であり，アンフェアでもある．Gattusoに対しては敵前逃亡というよりは，事前に白旗を揚げたものと勝手に解釈しているが，フェアに自らの間違いを認めてくれたことの証明に，秦論文に対する評価は高かったようである．

　積分不等式（propagation of error for integrated form）を用いると，サンゴ礁の炭素固定は世界中どこで測定しても正になると計算されているが，この式なしではＣＯ2収支計算の誤差が大きく，サンゴ礁がＣＯ2削減に役立っているかどうかわからなかったはずである．統計学の勝利といえる事件であった．

　地球惑星環境ばかりでなく，秦先生の学位論文にも貢献できたと思っている次第であるが，実は，秦論文で用いられた誤差解析を突き詰めていけば，高次元楕円体の射影問題に帰着することがわかっている．Gattusoの失敗は計算間違いもあったのであるがそれは二義的なもので，一義的には高次元楕円よりかなり大きい高次元直方体の誤差空間を考えていることに基づいているのである．このことが新たな展開をもたらすことになった．

　小生はやったこと，考えたこと，調べたことなどほとんどすべてについて原稿用紙３０～５０枚程度／週にまとめてＨＰにアップロードするよう心掛けている．ｎ次元楕円を２次元平面や３次元空間に正射影する方法も例にもれずＨＰ上に公開したところ，秋田大学・工学資源学研究科・ロボティクス・福祉工学講座の佐々木誠先生（makoto@control.mech.akita-u.ac.jp）より，この投影法が生体工学・ロボット工学の分野でも有用であるという情報が寄せられた．

　たとえば，ロボットアームを操作するにはｘ方向・ｙ方向・ｚ方向の速度，ｘ軸まわり・ｙ軸まわり・ｚ軸まわりの角速度を同時にコントロールしなければならない．これを「６軸制御」というのだそうだが，その際，６次元楕円が必要になるとのことであった．小生からすればひょうたんよりコマで，いろいろな使い道があるものだと感心したが，佐々木先生にとっても渡りに船・棚からボタ餅であったに違いない．

　ロボットの動作制御は３次元の問題ではないことがおわかり頂けたと思うが，ｎ次元楕円は直接には見ることのできない高次元図形であるから，６次元楕円の視覚化プログラムによって，イメージの理解が助けられるはずである．昔から「百聞は一見にしかず」といわれているが，実際どのように投影されるかはコラム「ロボットアームと６次元楕円体」を参照願いたい．こんな簡単な図がこれまで描けなかったというのは不思議な気もするが，ともあれ，佐々木先生によって，車イスの設計に６次元楕円評価法が応用されることとなった．

　　(1)６次元楕円の三面図（正面図，平面図，側面図）から，車いすの取っ手（ハンドリム）が八の字形になっていればよいということがわかる．このことはこれまで経験的には知られていたものの，理論的な裏付けがなっかたそうである．

　　(2)楕円の示す操作性が人の運動特性をほぼ表現できているという適合性が得られた．生体データとの整合性に関するこの結果は，筋・骨格系も含めて人の関節が球体に近い構造で近似できるためと推察されるが，佐々木先生の研究は確率楕円を生体データに適合させることの意味づけを行ったものと解釈される．

　　(3)また，佐々木先生の予稿集を読んでみて初めて知ったのであるが，いまある車イスは最小の人力で最大の操作性を発揮できるような理論的な設計がなされておらず，機能的には最適とはいいがたい．そこで，たとえば，筋力の衰えた高齢者に対して，個人個人の筋力や腕の長さに合わせた車イスを与えることができれば，その人の生活基盤を支えるのにかなり有効に働いてくれると思われた．

　佐々木先生の車イスへの応用によって，これまで多分に経験則的なアイディアのもとに構成されていてロジカル設計でなかった車イスの改良が期待でき，画一的なレディーメイドではなく，オーダーメイド設計への道が開かれたというわけである．

　秦先生の研究に端を発したことがｎ次元楕円を投影するという数学的な形に純化したことについて書き連ねてきたが，ヤコビアン（最小２乗法でいうと分散共分散行列に相当するもの）を与えてると，任意の次元の楕円を描くことが可能になる．

　これによって最も力の伝わりやすい方向などが評価できるようになるのであるが，ｎ次元楕円は現在車いすの設計に応用されていて，これまで経験的でしかなかった設計に初めて理論的な設計が導入され，設計の歴史に変革をもたらしたというのが秋田大学の佐々木先生の談である．

　車イスの場合，ヒトの腕の作業に応じて車イスを設計したが，ロボットアームの設計では，逆問題すなわち作業量を最小とするようにアームの腕の長さなどを設計する必要がある．ただし，速度空間を論ずる上で，ｎ次元楕円体よりもｎ次元直方体の方が厳密であることは確かであって，その点がロボット工学の観点からみた多面体の強みになっている．このことについてはコラム「ロボットアームとｎ次元直方体」をご参照願いたい．

　しかし，ロボットの動作が生体のように楕円体とならず，多面体（直方体）になるのは制御に無駄が多いからであって，逆にいえば，手術用ロボットとか２足歩行ロボットは，動作制御を多面体から楕円体に近づけることによって実現されると思われるのである．

　６次元楕円体がロボットアーム以外にも応用可能と思われる分野をあげておきたい．地震では東西・南北・天地方向の揺れ（平行移動）ばかりではなく，建物全体が捻れる（回転運動）ように動くのであるが，揺れるといっても左右に揺らぐばかりではなく，捻れながら揺れるのであるから，これも６次元振動の例である．

　ところで，ビル（高層ビル）の崩壊は揺れではなく主として捻れに原因しているらしいのだが，このことが明らかになったのは比較的最近のことである．１９７１年，ロサンゼルス大地震（パサディナ大地震）の際，日本の建築会社がビルのフロアに地震計を設置していて，この記録をもとに各階の揺れを解析したことが端緒になっているという．

　このことから，小生は６次元楕円が建物の耐震設計にも応用できるものと考えている．というよりは地震の振動解析といった方が正確かもしれないが，最も揺れやすい方向を楕円を用いて評価しようという試みは可能であろう．その際，振動楕円は各方向の揺れ速度・捻れ角速度あるいは揺れ加速度・捻れ角加速度を計算して描くことになるが，これは各振動間の相関も評価してくれるし，それになによりギザギザの線で描かれるスカラー的な振動よりも，振動方向を直接確認できるベクトル的な楕円という視覚的な強みもあるだろう．

　つまり，地震は６次元振動なのであるが，これが１つの楕円によって評価できるならば，強力な解析手段を提供してくれることになると思われるのである．

　統計解析では，特定の確率分布において，確率変数がある値以上または以下の値をとる確率（片側確率）と逆に片側確率を与えたときに対応する確率変数の値（パーセント点）を計算する必要が生する．一昔前までは，これらの値を求めるのに統計数値表をひくことが必要になり，検定や推定は大変手間のかかる作業であって，数表が利用できないときはまったくお手上げ状態となった．

　現在では，統計プログラムがこの作業を肩代わりしてくれるので，検定・推定は大変身近なものになっているが，正規分布・ｔ分布・Ｆ分布・χ2分布，さらに非心χ2分布・非心ｔ分布・非心Ｆ分布の片側確率やそのパーセント点を計算するのは，もっぱら近似関数によっている．

　近似関数であるから計算速度は申し分ないが，計算精度は高々３桁（相対誤差％オーダー）が限界であろう．そこで，精度６桁以上を目標にした確率分布の計算プログラムを作ることにした．いまから３年前のことである．

　幸い，超幾何関数を用いることによってこのような性能の確率分布の計算プログラムを完成させることができた．しかし，よくよく考えてみると，統計解析にかけるようなデータの場合，もともとその信頼度は高くないのが普通であって，このような高精度計算は無用の長物である．ところが，超幾何関数を用いたこの経験がのちのち活きてくることとなった．

　Ｘ線，γ線などの電磁波はそれぞれの線スペクトルに固有の幅と分布をもっていて，光の線スペクトルのようなコーシー分布を示すものを分光器で測定したとすると，分光器には固有の分解能があり，それは正規分布で近似できることが多いわけであるから，測定したスペクトルの分布はコーシー分布と正規分布を合成したものになる．正規分布（自由度が無限大のｔ分布）は頂点が丸くすその減退が速いのに対し，コーシー分布（自由度１のｔ分布）は頂点が鋭くすそが広く，両者は両極端の形をしている．

として定義される．この式は量子力学，数理生物学，赤外線分析，Ｘ線回折，クロマトや反応工学および多くの物理現象にわたって現れる普遍的関係式となっている．

　スペクトル曲線は，ローレンツ型（コーシー分布）でもガウス型（正規分布）でもなく，両者が混合した中間の形（フォークト型）になるのであるが，この関数

はフォークト（Voigt）関数と呼ばれ，分光学の分野では，実測のスペクトルデータを curve fitting するときに使われる．

　フォークト関数は積分関数を含んでいるが，台形則，シンプソン則などの区分求積法では要求される精度に到達せず，このことがスペクトル線の信号解析を困難にしている．

　　(1)計算時間を短くするためには複素誤差関数の級数展開で近似値を得る必要があるが，精度の点で問題があること，

　　(2)実験データとのカーブフィットを行う際，関数の微分（Jacobian行列）を求めると都合がよいのであるが，Voigt関数の微分が簡単には求められないので，数値微分することになるが，それでは精度がでないこと，

　外山先生が所望しているのは，Voigt関数を数値的にではなくて，解析的に表現するのが目的であり，高精度計測に必要とされる有効数字は６桁～１２桁であった．これらの点を解決すべく，精度が高く計算時間が短くてなおかつコーディングしやすい方法がないかと探したり考えたりしてみて，超幾何関数，放物柱関数，あるいは，複素誤差関数を用いた計算法に行き当たった．２年前のことである．

　しかし，計算精度を１０００倍にするために計算速度が１０００倍になったとしたら，これは実用プログラムとしては失敗作であろう．計算所要時間を１０倍以内に押さえるためには１００倍も速い計算方法をひねりださなければならないのである．無論，その過程においてストレスがないわけではないが，思うがままに組み立てることができたら意味はないし，壁に突き当たって頭を磨り減らして考え込んた末に，時のたつのも忘れ，考え始めると止められなくなってしまうことこそ醍醐味であり，創造の楽しみも苦しみも十分に味わえるのである．

　この過程で，鈴鹿高専の奥井重彦先生より，h(z)の超幾何級数展開の方法をご教示頂いたことが大きくものをいってプログラムを完成させることができたのだが，超幾何関数にクンマー変換を施したものが，精度的にも収束半径的にも最も優れていた．

　また，これらはいずれもVoigt関数のベキ級数展開に基づくものであって，とくにピーク付近（最も重要な部分）では申し分ない精度がでているものの，その反面，収束域が狭いという欠点が指摘された．そこで，ｘが大きいところのフォークト関数の計算を正確に行うために，漸近展開，漸近展開の連分数展開，ガウス・エルミート則（エルミート関数の零点を分点とし，分点におけるf(t)の値に重みを掛け補間する公式）による数値積分も試みた．

　一般に，連分数展開は速度的にも精度的にもよい計算法と信じられている節があるが，連分数展開は計算の手間に比して精度がよくないという期待はずれの結果となった．連分数展開にとっては悲観的な見方になるが，高精度計算が必要なときは，ベキ級数展開のほうがよいので，フォークト関数の高精度計算では２つの方法を組み合わせること，すなわち，ｘの小さいところで正確な方法（ベキ級数）とｘの大きいところで正確な方法（漸近展開＋連分数変換）を切り替えることが現実的であり，かつ，正当と考えられた．

　どこをその境にするかは問題があるのだが，外山先生によると，このとき作成したプログラムは，従来のプログラムと比較しても，精度面では圧倒的に有利で，速度（計算所要時間）の点では同程度だったそうである．

　分光現象と一口にいっても様々な種類のものがある．小生は大学院時代，微量元素の分析に携わっていたことがあるが，微量元素の分析には主として原子吸光やプラズマ発光が使われる．原子吸光やプラズマ発光のように元素の励起に必要なエネルギー測定法とは違って，微弱な分光現象を扱うときはフォークト関数が必要になる．

　たとえば，ラマン分光では分子に側鎖がついているときといないときの分子振動の差を検出する必要があるのだが，比喩的にいうならば，太鼓の膜に蝿がとまっているときといないときのかすかな音の違いを聞き分ける必要があるのである．

　しかし，フォークト関数は歯がたたない関数として諦めざるを得ず，その当時は苦肉の策として自由度２か３か４のｔ分布を使って代用するほかになかったのである．この顛末については，コラム「フォークト関数の計算」に掲げたが，フォークト関数の計算は小生にとっていわば青春の夢（Jugendtraum）といってよいものであろう．２０余年ぶりにやっと解決したわけである．

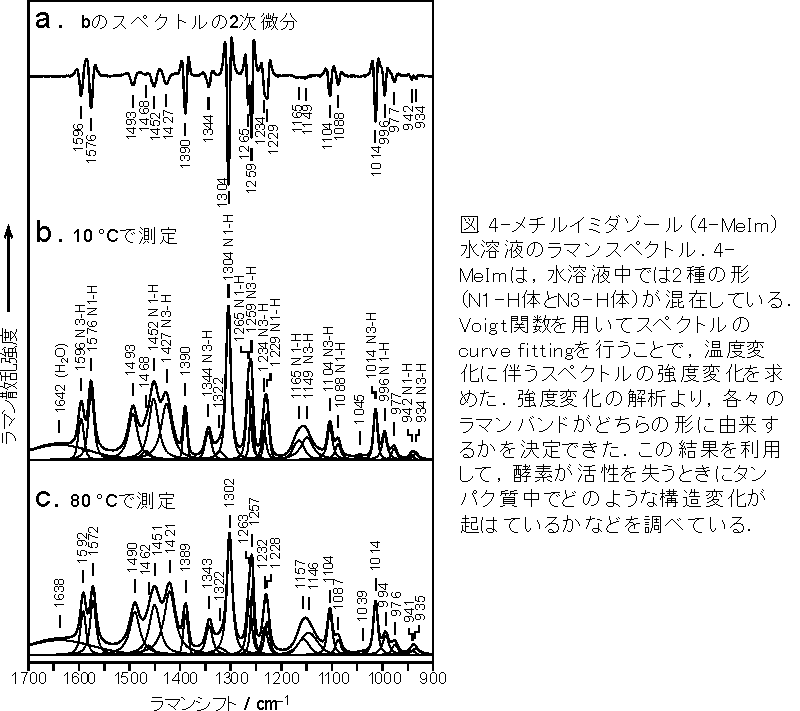
　最後に，フォークト関数がいかに精密計測に役立っているかを示す例として，外山先生の論文よりラマン分光に対するフォークト関数のアテハメ例を引用して締めくくることにしたい．

　今回のコラムでは，統計学の応用領域を拡大創建することができた３つの例を掲げたが，統計学そのものは各研究分野を横断的にまたがる学問であって，いわゆる専門分野のような境界をもっていない．その意味では境界領域とか学際的と呼ばれる形の研究を進めなければならない．

　数学，物理学，化学，生物学，遺伝学，心理学，経済学，情報科学，言語学，免疫学，コンピュータ科学などで対象となっているテーマに，細分化された各専門を越えて横断的に取り込んでいこうとする学際性を重んじた研究が奨励される所以でもある．

　学際的な科学研究を目指すには，専門分野にとらわれることなく柔軟な姿勢で積極的に専攻外の知識も融合すること，広い視野にたってかけ離れた分野でいま必要とされているものは何かという情報を収集することが要求される．小生の場合はインターネットを使って各分野から情報を得ていて，研究上生じた問題に応じて新たな方法論を開発し，フィードバックすることが主な仕事になるが，これについてはこれまでの経験とインスピレーション，イマジネーションで new methodology を生み出すしかないのである．

　何年か前までは病理学なる学問を人一倍こつこつと勉強していた男が，それに飽きたらず，実際のデータ解析を通じてふと思いついた種を育むうちに，数学ことに数理統計に魅せられて，学術雑誌に論文を公表したり，とうとう単行書まで上梓するに至った．

　がんセンターの研究所に籍を置いてからも，コンピュータ上で実験可能な統計理論の応用ということを日々の研究課題としている．電子メールやホームページを利用したＱ＆Ａにも取り組んでいるが，もちろん，注文に応じて問題解決の手助けをするだけでは物足りない．頭をひねってあれこれの理論をあみだし，具体的な公式を提示し伝えることこそが，自分に課せられた使命であり天職だと考えている．

　これらの理論や公式は幸い好評裡に迎えられ，多数の研究者に利用されているが，がん研究所という研究環境の風圧を堪え忍びながら，人目をはばかって肩身の狭い思いをしてまでやり抜くことにも限界はある．自分自身が無用の長物と化しているという悩み多きこの頃である．