楕円近似と題しているが，今回のコラムで扱うのは「円近似」である．円近似は楕円近似に比べて数段易しい問題である．なぜなら，求める円の中心を（ｘ0，ｙ0），半径をｒとして，モデル式は

　　ｆ（ｘ，ｙ）＝（ｘ−ｘ0）^2＋（ｙ−ｙ0）^2−ｒ^2＝０

の形に書けるので，多変量の線形最小２乗法が適用可能となるからである．もっとも，非線形のプログラムでも線形最小２乗法は解けるわけであるから（その３）に掲げたプログラムを改良して円近似を試みることにした．

　

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　

［１］プログラム

　

1000 '

1010 ' **** circular approximation ****

1020 '　　　　　　　　　　　　　2003/01/15 (C) ｻﾄｳ ｲｸﾛｳ

1030 SCREEN 3,0:CONSOLE ,,0,1

1040 CLS 3:WIDTH 80,25:COLOR 6

1050 GOSUB *INITIALIZE

1060 GOSUB *READ.DATA

1070　GOSUB *INIT.VAL :L2$="LINEAR METHOD"

1080　GOSUB *EXECUTION:L2$="GAUSS-NEWTON METHOD"

1090 GOSUB *SCATTER.DIAGRAM

1100 GOSUB *REPORT

1110 END

1120 '

1130 ' *** 初期設定 ***

1140 '

1150 *INITIALIZE:

1160 M=3:' No. of parameters

1170 DIM P(M),W(M)

1180 DIM A(M)

1190 DIM P0(M),P1(M),DP(M)

1200 DIM AZ(M,M),BZ(M,M)

1210 DIM HESSE(M,M)

1220 DIM SD(M),SE(M)

1230 DIM COV(M,M)

1240 '

1250 NV=2:' No. of independent variables

1260 DIM X(NV)

1270 DIM AVE(NV),DEV(NV),SEM(NV)

1280 DIM XMAX(NV),XMIN(NV)

1290 FOR J=0 TO NV

1300　 XMAX(J)=-1E+10:XMIN(J)=1E+10

1310 NEXT J

1320 '

1330 RX=.7:RY=.8:BOX=1:KIND=1:POWER=0

1340 IX=.7:IY=.8:MARK=1:CLR=2:DRAW.COLOR=4

1350 TXT.COLOR=6:GRP.COLOR=5:REF.COLOR=6

1360 SCALE.KIND=1:PLOT=1

1370 PI=3.14159

1380　JX=.709:JY=1

1390 'JX=1　 :JY=1

1400 RX=IX*JX:RY=IY*JY

1410 '

1420 'FORM$="((X(1)-P(1))/P(3))^2+((X(2)-P(2))/P(3))^2-1"

1430　FORM$="(X(1)-P(1))^2+(X(2)-P(2))^2-P(3)^2"

1440 RETURN

1450 '

1460 ' *** DEFINED EQUATION ***

1470 '

1480 *DEFINE.FORMULA:

1490 'DEF FNY(X)=((X(1)-P(1))/P(3))^2+((X(2)-P(2))/P(3))^2-1

1500　DEF FNY(X)=(X(1)-P(1))^2+(X(2)-P(2))^2-P(3)^2

1510 RETURN

1520 '

1530 *DEFINE.FORMULA2:

1540 ON J GOSUB *J1,*J2,*J3

1550 RETURN

1560 '

1570 '*J1:DEF FNJ(X)=-2*(X(1)-P(1))/P(3)^2:RETURN

1580 '*J2:DEF FNJ(X)=-2*(X(2)-P(2))/P(3)^2:RETURN

1590 '*J3:DEF FNJ(X)=-2*((X(1)-P(1))^2+(X(2)-P(2))^2)/P(3)^3:RETURN

1600　*J1:DEF FNJ(X)=-(X(1)-P(1))*2:RETURN

1610　*J2:DEF FNJ(X)=-(X(2)-P(2))*2:RETURN

1620　*J3:DEF FNJ(X)=-P(3)*2　　　 :RETURN

1630 '

1640 ' *** データ読み込み ***

1650 '

1660 *READ.DATA:

1670 CLS 3

1680 RESTORE *D

1690 READ N1

1700 'DFILE$="DATA01.TXT"

1710 'OPEN DFILE$ FOR INPUT AS #1

1720 'INPUT #1,N1

1730 '

1740 DIM XX1(NV,N1),YH(N1),WT(N1)

1750 DIM Y1(N1),E1(N1)

1760 DIM Z1(N1)

1770 DIM JACOBI(M,N1)

1780 FOR J=1 TO N1:WT(J)=1:NEXT J

1790 '

1800 FOR I=1 TO N1

1810　 FOR J=1 TO NV

1820　　 READ XX1(J,I)

1830　　'INPUT #1,XX1(J,I)

1840　 NEXT J

1850 NEXT I

1860 'CLOSE #1

1870 '

1880 PRINT "ただいまデータの取り込み中"

1890 FOR I=1 TO N1

1900 PRINT "*";

1910 Y1(I)=0

1920 X(0)=Y1(I)

1930 FOR J=1 TO NV

1940　 X(J)=XX1(J,I)

1950 NEXT J

1960 'Z1(I)=1

1970　Z1(I)=X(1)*X(1)+X(2)*X(2)

1980 GOSUB *CALCULATE

1990 NEXT I

2000 '

2010 FOR J=0 TO NV

2020　 SS=DEV(J)-AVE(J)*AVE(J)/N1

2030　 DEV(J)=SQR(SS/(N1-1))

2040　 SEM(J)=DEV(J)/SQR(N1)

2050　 AVE(J)=AVE(J)/N1

2060 NEXT J

2070 RETURN

2080 '

2090 ' *** CALCULATE ***

2100 '

2110 *CALCULATE:

2120 FOR J=0 TO NV

2130　 IF XMAX(J)<X(J) THEN XMAX(J)=X(J)

2140　 IF XMIN(J)>X(J) THEN XMIN(J)=X(J)

2150　 AVE(J)=AVE(J)+X(J)

2160　 DEV(J)=DEV(J)+X(J)*X(J)

2170 NEXT J

2180 RETURN

2190 '

2200 ' *** 非線形最小２乗法 ***

2210 '

2220 *EXECUTION:

2230 PRINT:PRINT "ただいま計算中"

2240 GOSUB *GAUSS.NEWTON

2250 GOSUB *FINAL

2260 RETURN

2270 '

2280 ' *** GAUSS-NEWTON METHOD ***

2290 '

2300 *GAUSS.NEWTON:

2310　LMAX=50

2320 'LMAX=500

2330 LOOP=0

2340 GOSUB *RESIDUAL:SO=SS

2350 GOSUB *TEMPORARY

2360 '

2370 GOSUB *JACOBIAN

2380 GOSUB *HESSIAN

2390 FOR I=1 TO M:P1(I)=P(I):NEXT I

2400 GOSUB *MARQUARDT

2410 GOSUB *UPDATE

2420 GOSUB *TRANSFORM

2430 '

2440 IF SN<SO THEN 2460

2450 FOR I=1 TO M:DP(I)=DP(I)/2:NEXT I:GOSUB *TRANSFORM:' [DAMPING]

2460 GOSUB *CONVERGENCE:IF SW=0 THEN RETURN

2470 SO=SN:IF LOOP<LMAX THEN 2370

2480 RETURN

2490 '

2500 ' ** X **

2510 '

2520 *JACOBIAN:

2530 FOR I=1 TO N1

2540　 FOR V=1 TO NV:X(V)=XX1(V,I):NEXT V

2550　 FOR J=1 TO M

2560　　 GOSUB *DEFINE.FORMULA2

2570　　 JACOBI(J,I)=FNJ(X)

2580　 NEXT J

2590 NEXT I

2600 GOSUB *JACOBIAN.SUB

2610 RETURN

2620 '

2630 ' ** Y **

2640 '

2650 *JACOBIAN.SUB:

2660 FOR I=1 TO N1

2670　 FOR V=1 TO NV:X(V)=XX1(V,I):NEXT V

2680　 GOSUB *DEFINE.FORMULA:YH=FNY(X)

2690　 E1(I)=Y1(I)-YH

2700　'E1(I)=SQR((X(1)-P(1))^2+(X(2)-P(2))^2)-ABS(P(3))

2710　 YH(I)=YH

2720 NEXT I

2730 '

2740 ' ** XT*Y **

2750 '

2760 FOR J=1 TO M

2770　 S=0

2780　 FOR I=1 TO N1

2790　　 S=S+JACOBI(J,I)*E1(I)*WT(I)

2800　 NEXT I

2810　 W(J)=S

2820 NEXT J

2830 RETURN

2840 '

2850 ' ** XT*X **

2860 '

2870 *HESSIAN:

2880 FOR M1=1 TO M

2890　 FOR M2=M1 TO M

2900　　 S=0

2910　　 FOR I=1 TO N1

2920　　　 S=S+JACOBI(M1,I)*JACOBI(M2,I)*WT(I)

2930　　 NEXT I

2940　　 HESSE(M1,M2)=S:HESSE(M2,M1)=S

2950　 NEXT M2

2960 NEXT M1

2970 NZ=M

2980 RETURN

2990 '

3000 ' ** MARQUARDT **

3010 '

3020 *MARQUARDT:

3030 FOR I=1 TO M

3040　 FOR J=1 TO M:AZ(I,J)=HESSE(I,J):NEXT J

3050 NEXT I

3060 RETURN

3070 '

3080 ' ** UPDATE **

3090 '

3100 *UPDATE:

3110 GOSUB *INVERSE:' (XT*X)^(-1)

3120 GOSUB *UPDATE.SUB

3130 RETURN

3140 '

3150 ' ** (XT*X)^(-1)*XT*Y **

3160 '

3170 *UPDATE.SUB:

3180 FOR J=1 TO M

3190　 S=0

3200　 FOR K=1 TO M

3210　　 S=S+BZ(J,K)*W(K)

3220　 NEXT K

3230　 DP(J)=S

3240 NEXT J

3250 RETURN

3260 '

3270 ' ** TRANSFORM of PARAMETERS **

3280 '

3290 *TRANSFORM:

3300 FOR I=1 TO M

3310　 P(I)=P1(I)+DP(I)

3320 NEXT I

3330 GOSUB *RESIDUAL:SN=SS

3340 RETURN

3350 '

3360 ' ** SUM of RESIDUALS **

3370 '

3380 *RESIDUAL:

3390 SS=0

3400 FOR K=1 TO N1

3410　 FOR V=1 TO NV:X(V)=XX1(V,K):NEXT V

3420　 GOSUB *DEFINE.FORMULA:YH=FNY(X)

3430　 SS=SS+WT(K)*(Y1(K)-YH)^2

3440　'E1(K)=SQR((X(1)-P(1))^2+(X(2)-P(2))^2)-ABS(P(3))

3450　'SS=SS+WT(K)*(E1(K))^2

3460 NEXT K

3470 RETURN

3480 '

3490 ' *** CHECK of CONVERGENCE ***

3500 '

3510 *CONVERGENCE:

3520 'EPS=.0001

3530　EPS=.001

3540 SW=0

3550 IF ABS((SN-SO)/SO)>EPS THEN SW=1

3560 GOSUB *TEMPORARY

3570 RETURN

3580 '

3590 ' *** TEMPORARY OUTPUT ***

3600 '

3610 *TEMPORARY:

3620 LOOP=LOOP+1

3630 CLS 3

3640 PRINT "LOOP=";LOOP

3650 PRINT

3660 PRINT "PARAMETERS: "

3670 FOR I=1 TO M

3680　 PRINT "P(";I;")=";P(I)

3690 NEXT I

3700 PRINT

3710 PRINT "RESIDUALS=";SS

3720 RETURN

3730 '

3740 ' *** FINAL OUTPUT ***

3750 '

3760 *FINAL:

3770 CLS 3

3780 PRINT "LOOP=";LOOP

3790 PRINT

3800 PRINT "PARAMETERS: "

3810 FOR I=1 TO M

3820　 PRINT "P(";I;")=";P(I)

3830 NEXT I

3840 PRINT

3850 PRINT "RESIDUALS=";SN

3860 '

3870 GOSUB *PROPAGATION

3880 PRINT

3890 PRINT "何かキーを押してください"

3900 WHILE INKEY$="":WEND

3910 RETURN

3920 '

3930 ' ** INVERSE MATRIX ( AZ==>BZ ) **

3940 '

3950 *INVERSE:' [GAUSS-JORDAN]

3960 FOR I=1 TO NZ

3970　 FOR J=1 TO NZ:BZ(I,J)=0:NEXT J

3980　 BZ(I,I)=1

3990 NEXT I

4000 FOR I=1 TO NZ

4010　 IZ=I

4020　 IF AZ(I,I)=0 THEN 4030 ELSE 4090

4030　 IZ=IZ+1:IF IZ>NZ THEN RZ=1:RETURN

4040　 IF AZ(IZ,I)=0 THEN 4030

4050　 FOR J=1 TO NZ

4060　　 SWAP AZ(I,J),AZ(IZ,J)

4070　　 SWAP BZ(I,J),BZ(IZ,J)

4080　 NEXT J

4090　 AII=AZ(I,I)

4100　 FOR J=1 TO NZ

4110　　 AZ(I,J)=AZ(I,J)/AII

4120　　 BZ(I,J)=BZ(I,J)/AII

4130　 NEXT J

4140　 FOR K=1 TO NZ

4150　　 AKI=AZ(K,I):IF K=I THEN 4200

4160　　 FOR J=1 TO NZ

4170　　　 AZ(K,J)=AZ(K,J)-AKI*AZ(I,J)

4180　　　 BZ(K,J)=BZ(K,J)-AKI*BZ(I,J)

4190　　 NEXT J

4200　 NEXT K

4210 NEXT I

4220 RZ=0

4230 RETURN

4240 '

4250 ' *** 係数の誤差変換 ***

4260 '

4270 *PROPAGATION:

4280 FOR IS=1 TO M

4290　 SD(IS)=SQR(ABS(BZ(IS,IS)*SN/(N1-M)))

4300　 SE(IS)=SD(IS)/SQR(N1)

4310　 '

4320　 FOR JS=IS TO M

4330　　 COV(IS,JS)=BZ(IS,JS)*SN/(N1-M):COV(JS,IS)=COV(IS,JS)

4340　 NEXT JS

4350 NEXT IS

4360 RETURN

4370 '

4380 ' *** SCATTER DIAGRAM ***

4390 '

4400 *SCATTER.DIAGRAM:

4410 CLS 3:WIDTH 80,25:COLOR 6

4420 DMIN=P(1)-P(3):DMAX=P(1)+P(3)

4430 IF DMAX<XMAX(1) THEN DMAX=XMAX(1)

4440 IF DMIN>XMIN(1) THEN DMIN=XMIN(1)

4450 GOSUB *LINER.SCALE:UO=SMIN:UL=SMAX:DU=DIF:SU=STP

4460 '

4470 DMIN=P(2)-P(3):DMAX=P(2)+P(3)

4480 IF DMAX<XMAX(2) THEN DMAX=XMAX(2)

4490 IF DMIN>XMIN(2) THEN DMIN=XMIN(2)

4500 GOSUB *LINER.SCALE:VO=SMIN:VL=SMAX:DV=DIF:SV=STP

4510 GOSUB *DRAW.AXIS

4520 GOSUB *DRAW.ELLIPSE:'GOSUB *GSAVE

4530 GOSUB *TEMP

4540 '

4550 CLS 3

4560 RETURN

4570 '

4580 ' *** 楕円 ***

4590 '

4600 *DRAW.ELLIPSE:

4610 'DRAW.COLOR=4

4620 WUO=UO:WUL=UL

4630 WVO=VO:WVL=VL

4640 WINDOW(WUO,-WVL)-(WUL,-WVO)

4650 VIEW(SX1,SY1)-(SX2,SY2)

4660 '

4670 GOSUB *CONTOUR

4680 '

4690 WINDOW(0,0)-(639,399)

4700 VIEW(0,0)-(639,399)

4710 RETURN

4720 '

4730 ' *** 輪郭 ***

4740 '

4750 *CONTOUR:

4760 CCC=P(3)

4770 X0=P(1):Y0=P(2)

4780 '

4790 G=0

4800 FOR ANGLE=0 TO 2*PI+.01 STEP PI/180

4810　 GX=CCC*COS(ANGLE)+X0

4820　 GY=CCC*SIN(ANGLE)+Y0

4830　 IF G=0 THEN PSET(GX,-GY),DRAW.COLOR:G=1

4840　 LINE-(GX,-GY),DRAW.COLOR

4850 NEXT ANGLE

4860 RETURN

4870 '

4880 ' *** 座標軸 ***

4890 '

4900 *DRAW.AXIS:

4910 CLS 3

4920 SX1=59:SY1=360*(1-RY):SX2=580*RX+59:SY2=360

4930 LINE(SX1,SY1)-(SX2,SY2),GRP.COLOR,B

4940 RR=3:GOSUB *X.SCALE2:GOSUB *X.REF2

4950 RR=3:GOSUB *Y.SCALE2:GOSUB *Y.REF2

4960 RR=3:GOSUB *DOT.PLOT

4970 GOSUB *TITLE.BACK2

4980 RETURN

4990 '

5000 ' *** 等分目盛り (X) ***

5010 '

5020 *X.SCALE2:

5030 CU=(SX2-SX1)/DU

5040 IF KIND=0 THEN KARA=-RR:MADE=0

5050 IF KIND=1 THEN KARA=0　:MADE=RR

5060 IF KIND=2 THEN KARA=-RR:MADE=RR

5070 FOR K=0 TO DU

5080　 LINE(CU*K+SX1,SY2+KARA)-(CU*K+SX1,SY2+MADE),GRP.COLOR

5090　 LINE(CU*K+SX1,SY1-KARA)-(CU*K+SX1,SY1-MADE),GRP.COLOR

5100 NEXT K

5110 RETURN

5120 '

5130 ' *** 参照値の記入 (X) ***

5140 '

5150 *X.REF2:

5160 REF.COLOR=6

5170 UW=UL-UO

5180 FOR K=0 TO DU STEP SU

5190　 F=UW*K/DU+UO:F$=STR$(F)

5200　 IF F>=0 THEN F$=MID$(F$,2)

5210　 FL=LEN(F$)

5220　 FOR L=1 TO FL

5230　　 GX=CU*K+59-FL*8/2+(L-1)*8:GY=23*16

5240　　 PUT(GX,GY),KANJI(ASC(MID$(F$,L,1))),PSET,REF.COLOR,0

5250　 NEXT L

5260 NEXT K

5270 RETURN

5280 '

5290 ' *** 等分目盛り (Y) ***

5300 '

5310 *Y.SCALE2:

5320 CV=(SY2-SY1)/DV

5330 IF KIND=0 THEN KARA=0　:MADE=RR

5340 IF KIND=1 THEN KARA=-RR:MADE=0

5350 IF KIND=2 THEN KARA=-RR:MADE=RR

5360 FOR K=0 TO DV

5370　 LINE(SX1+KARA,SY2-CV*K)-(SX1+MADE,SY2-CV*K),GRP.COLOR

5380　 LINE(SX2-KARA,SY2-CV*K)-(SX2-MADE,SY2-CV*K),GRP.COLOR

5390 NEXT K

5400 RETURN

5410 '

5420 ' *** 参照値の記入 (Y) ***

5430 '

5440 *Y.REF2:

5450 REF.COLOR=6

5460 VW=VL-VO

5470 FOR K=0 TO DV STEP SV

5480　 F=VW*K/DV+VO:F$=STR$(F)

5490　 IF F>=0 THEN F$=MID$(F$,2)

5500　 FL=LEN(F$)

5510　 FOR L=1 TO FL

5520　　 GX=48-FL*8+(L-1)*8:GY=360-CV*K-8

5530　　 PUT(GX,GY),KANJI(ASC(MID$(F$,L,1))),PSET,REF.COLOR,0

5540　 NEXT L

5550 NEXT K

5560 RETURN

5570 '

5580 ' *** プロット ***

5590 '

5600 *DOT.PLOT:

5610 WUO=UO:WUL=UL

5620 WVO=VO:WVL=VL

5630 WX=WUL-WUO

5640 BX=(WUL*SX1-WUO*SX2)/WX

5650 AX=(SX2-SX1)/WX

5660 WY=WVL-WVO

5670 BY=(WVL*SY2-WVO*SY1)/WY

5680 AY=(SY1-SY2)/WY

5690 '

5700 FOR I=1 TO N1

5710 X=XX1(1,I):Y=XX1(2,I)

5720 XX=AX*X+BX

5730 YY=AY*Y+BY

5740 CIRCLE(XX,YY),RR,1

5750 PAINT(XX,YY),CLR,1

5760 CIRCLE(XX,YY),RR,CLR

5770 NEXT I

5780 RETURN

5790 '

5800 ' *** タイトル ***

5810 '

5820 *TITLE.BACK2:

5830 LX=INT((580*RX+59)/8)

5840 LY=INT(360*(1-RY)/16)

5850 LZ=INT((290*RX+59)/8)

5860 L1$="circular approximation by "

5870 'L2$="GAUSS-NEWTON METHOD"

5880 L$=L1$+L2$

5890 LOCATE LZ-LEN(L$)\2,LY-3:PRINT L$

5900 '

5910 LOCATE LX+3,LY:PRINT "PARAMETERS: "

5920 FOR K=1 TO M

5930　 V$="P"+MID$(STR$(K),2)+"="

5940　 LOCATE LX+3,LY+K+1:PRINT V$;:PRINT P(K)

5950 NEXT K

5960 RETURN

5970 '

5980 *TEMP:

5990 LOCATE 0,24:PRINT "何かキーを押してください";:WHILE INKEY$="":WEND

6000 RETURN

6010 '

6020 ' *** 平均律スケールの作成 ***

6030 '

6040 *LINER.SCALE:

6050 DIM INTERVAL(10)

6060 RESTORE *REF.INTERVAL

6070 FOR I=1 TO 10:READ INTERVAL(I):NEXT I

6080 MAX.INTERVAL=10

6090 '

6100 ARGUMENT=DMAX-DMIN

6110 GOSUB *SCALE.RTN

6120 INDEX=CMP

6130 INTERVAL=INTERVAL(INDEX)*EP

6140 LO=INT(DMIN/INTERVAL)

6150 HI=-INT(-DMAX/INTERVAL)

6160 WHILE (HI-LO)>MAX.INTERVAL

6170　 INDEX=INDEX+1

6180　 IF INDEX>10 THEN INDEX=1:EP=EP*10

6190　 INTERVAL=INTERVAL(INDEX)*EP

6200　 LO=INT(DMIN/INTERVAL)

6210　 HI=-INT(-DMAX/INTERVAL)

6220 WEND

6230 SMIN=LO*INTERVAL

6240 SMAX=HI*INTERVAL

6250 DIF=HI-LO

6260 STP=1

6270 ERASE INTERVAL

6280 RETURN

6290 '

6300 ' ** ラベリング関数 **

6310 '

6320 *SCALE.RTN:

6330 'RE=INT(LOG(ARGUMENT)/LOG(10))

6340 RE=INT(LOG(CDBL(ARGUMENT))/LOG(10#))

6350 'EP=10^RE

6360 EP=VAL("1E"+STR$(RE)):'[EXPONENT PART]

6370 MP=ARGUMENT/EP　　　 :'[MANTISSA PART]

6380 FMP=INT(MP)　:'[FLOORING MANTISSA PART]

6390 CMP=-INT(-MP):'[CEILING MANTISSA PART]

6400 RETURN

6410 '

6420 ' ** 参照間隔 **

6430 '

6440 *REF.INTERVAL:

6450 DATA .1,.2,.5,.5,.5,1,1,1,1,1

6460 '

6470 ' *** REPORT ***

6480 '

6490 *REPORT:

6500 CLS 3

6510 PRINT:PRINT

6520 PRINT "DATA No.=";N1

6530 PRINT

6540 PRINT " "," MEAN"," S.D."," MIN"," MAX"

6550 FOR I=1 TO NV

6560 PRINT "X("+MID$(STR$(I),2)+")",AVE(I),DEV(I),XMIN(I),XMAX(I)

6570 NEXT I

6580 PRINT:PRINT

6590 '

6600 PRINT "[ DEFINED EQUATION ]"

6610 PRINT "Y= ";FORM$

6620 '

6630 GOSUB *CEF.CONFIDENCE

6640 GOSUB *TEMP.STOP

6650 '

6660 CLS 3

6670 PRINT:PRINT "残差"

6680 PRINT " No."," OBSERVED Y"," EXPECTED Y"," RESIDUAL"

6690 FOR I=1 TO N1

6700　 FOR V=1 TO NV:X(V)=XX1(V,I):NEXT V

6710　 GOSUB *DEFINE.FORMULA:YH=FNY(X)

6720　 PRINT I,Y1(I),YH,Y1(I)-YH

6730　 IF (I MOD 20)=0 THEN PRINT

6740 NEXT I

6750 PRINT

6760 GOSUB *TEMP.STOP

6770 RETURN

6780 '

6790 *CEF.CONFIDENCE:

6800 PRINT

6810 PRINT "回帰係数とその９５％信頼区間"

6820 DF1=1:DF2=N1-M

6830 GOSUB *CEF.CONFIDENCE.SUB

6840 PRINT:PRINT

6850 RETURN

6860 '

6870 *CEF.CONFIDENCE.SUB:

6880 FOR J=1 TO M

6890　 P$="P("+MID$(STR$(J),2)+")= "

6900　 PRINT P$;:PRINT P(J);

6910　 IF SD(J)=0 THEN PRINT:GOTO 6940

6920　 GOSUB *CEF.ERROR

6930　 PRINT TAB(30);"S.E.=";SE(J)　　　　　　　　　　　　　　　　　　　　　　　　　　　　　;TAB(50);P(J)-SE(J)*UUT;" - ";P(J)+SE(J)*UUT

6940 NEXT J

6950 RETURN

6960 '

6970 *TEMP.STOP:

6980 PRINT "何かキーを押してください"

6990 WHILE INKEY$="":WEND

7000 RETURN

7010 '

7020 ' *** ERROR of COEFFICIENT ***

7030 '

7040 *CEF.ERROR:

7050 PP=.05 :GOSUB *F.PERCENT

7060 UUT=SQR(UUF)

7070 RETURN

7080 '

7090 ' ** NORMAL DISTRIBUTION **

7100 '

7110 *NORMAL.PERCENT:

7120 XXX=-LOG(4*PP*(1-PP))

7130 UUN=SQR(XXX*(2.06118-5.72622/(XXX+11.6406)))

7140 IF PP>.5 THEN UUN=-UUN

7150 RETURN

7160 '

7170 ' ** T-DISTRIBUTION **

7180 '

7190 *T.PERCENT:

7200 GOSUB *NORMAL.PERCENT

7210 UUN=ABS(UUN)

7220 UU2=UUN*UUN

7230 AA1=(UU2+1)/DF/4

7240 AA2=((5*UU2+16)*UU2+3)/96/DF/DF

7250 AA3=(((3*UU2+19)*UU2+17)*UU2-15)/384/DF/DF/DF

7260 UUT=UUN*(1+AA1+AA2+AA3)

7270 IF PP>.5 THEN UUT=-UUT

7280 RETURN

7290 '

7300 ' ** F-DISTRIBUTION **

7310 '

7320 *F.PERCENT:

7330 IF DF1=1 THEN DF=DF2:PP=PP/2:GOSUB *T.PERCENT　　　　　　　　　　　　　　　　　　　　　　　　:UUF=UUT^2:PP=PP*2:RETURN

7340 IF DF2=1 THEN DF=DF2:PP=(1-PP)/2:GOSUB *T.PERCENT　　　　　　　　　　　　　　　　　　　　　　:UUF=1/UUT^2:PP=1-PP*2:RETURN

7350 IF DF1=2 THEN UUF=DF2/2*(PP^(-2/DF2)-1):RETURN

7360 IF DF2=2 THEN UUF=2/DF1/((1-PP)^(-2/DF1)-1):RETURN

7370 AA=2/9/DF1:BB=2/9/DF2:CC=1-AA:DD=1-BB

7380 GOSUB *NORMAL.PERCENT

7390 UUF=CC*DD+UUN*SQR(CC*CC*BB+DD*DD*AA-AA*BB*UUN*UUN)

7400 UUF=(UUF/(DD*DD-BB*UUN*UUN))^3

7410 RETURN

7420 '

7430 ' ** CHI-SQUARE DISTRIBUTION **

7440 '

7450 *CHI2.PERCENT:

7460 IF DF=1 THEN PP=PP/2:GOSUB *NORMAL.PERCENT　　　　　　　　　　　　　　　　　　　　　　　　　:UUX=UUN*UUN:PP=PP*2:RETURN

7470 IF DF=2 THEN UUX=-2*LOG(PP):RETURN

7480 GOSUB *NORMAL.PERCENT

7490 UUX=2/(9*DF)

7500 UUX=1-UUX+UUN*SQR(UUX)

7510 UUX=UUX^3*DF

7520 RETURN

7530 '

7540 ' ** VRAM SAVE **

7550 '

7560 *GSAVE:

7570 FL$="b:circle"

7580 DEF SEG=&HA000

7590 BSAVE FL$+".CHR",&H0,&HFA0

7600 DEF SEG=&HA200

7610 BSAVE FL$+".ATR",&H0,&HFA0

7620 DEF SEG=&HA800

7630 BSAVE FL$+".BLU",&H0,&H7D00

7640 DEF SEG=&HB000

7650 BSAVE FL$+".RED",&H0,&H7D00

7660 DEF SEG=&HB800

7670 BSAVE FL$+".GRN",&H0,&H7D00

7680 RETURN

7690 '

7700 ' ** 係数変換 **

7710 '

7720 '*P2A:

7730 K=P(3)^2-P(1)^2-P(1)^2

7740 A1=1/K

7750 A2=-P(1)*2/K

7760 A3=-P(2)*2/K

7770 RETURN

7780 '

7790 '*A2P:

7800 A1=A(1):A2=A(2):A3=A(3)

7810 P(1)=-A2/A1/2

7820 P(2)=-A3/A1/2

7830 P(3)=SQR(P(1)^2+P(2)^2+1/A1)

7840 RETURN

7850 '

7860　*P2A:

7870 P1=P(1):P2=P(2):P3=P(3)

7880 A(1)=P1*2

7890 A(2)=P2*2

7900 A(3)=P3*P3-P1*P1-P2*P2

7910 RETURN

7920 '

7930　*A2P:

7940 A1=A(1):A2=A(2):A3=A(3)

7950 P(1)=A1/2

7960 P(2)=A2/2

7970 P(3)=SQR(P(1)*P(1)+P(2)*P(2)+A3)

7980 RETURN

7990 '

8000 ' *** DEFINED EQUATION ***

8010 '

8020 *DEFINE.FORMULA3:

8030 ON L GOSUB *L1,*L2,*L3

8040 RETURN

8050 '

8060 '*L1:DEF FNJ(X)=X(1)*X(1)+X(2)*X(2):RETURN

8070 '*L2:DEF FNJ(X)=X(1)　　　　　　　 :RETURN

8080 '*L3:DEF FNJ(X)=X(2)　　　　　　　 :RETURN

8090　*L1:DEF FNJ(X)=X(1)　　　　　　　 :RETURN

8100　*L2:DEF FNJ(X)=X(2)　　　　　　　 :RETURN

8110　*L3:DEF FNJ(X)=1　　　　　　　　　:RETURN

8120 '

8130 ' ** 初期値 **

8140 '

8150 *INIT.VAL:

8160 GOSUB *LEAST.SQUARES

8170 GOSUB *A2P

8180 GOSUB *GAUSS.NEWTON.ERROR

8190 RETURN

8200 '

8210 ' ** XT*X **

8220 '

8230 *LEAST.SQUARES:

8240 FOR M1=1 TO M

8250　 FOR M2=M1 TO M

8260　 S=0

8270　　 FOR I=1 TO N1

8280　　　 FOR V=1 TO NV:X(V)=XX1(V,I):NEXT V

8290　　　 L=M1:GOSUB *DEFINE.FORMULA3:L1=FNJ(X)

8300　　　 L=M2:GOSUB *DEFINE.FORMULA3:L2=FNJ(X)

8310　　　 S=S+WT(I)*L1*L2

8320　　 NEXT I

8330　 AZ(M1,M2)=S:AZ(M2,M1)=S

8340　 NEXT M2

8350 NEXT M1

8360 NZ=M

8370 '

8380 ' ** (XT*X)^(-1) **

8390 '

8400 GOSUB *INVERSE

8410 '

8420 ' ** XT*Y **

8430 '

8440 FOR J=1 TO M

8450　 S=0

8460　 FOR I=1 TO N1

8470　　 FOR V=1 TO NV:X(V)=XX1(V,I):NEXT V

8480　　 L=J:GOSUB *DEFINE.FORMULA3:L1=FNJ(X)

8490　　 S=S+WT(I)*L1*Z1(I)

8500　 NEXT I

8510　 W(J)=S

8520 NEXT J

8530 '

8540 ' ** (XT*X)^(-1)*XT*Y **

8550 '

8560 FOR J=1 TO M

8570　 S=0

8580　 FOR K=1 TO M

8590　　 S=S+BZ(J,K)*W(K)

8600　 NEXT K

8610　 A(J)=S

8620 NEXT J

8630 RETURN

8640 '

8650 ' ** GAUSS-NEWTON ERROR **

8660 '

8670 *GAUSS.NEWTON.ERROR:

8680 GOSUB *RESIDUAL:SN=SS

8690 GOSUB *JACOBIAN

8700 GOSUB *HESSIAN

8710 FOR I=1 TO M

8720　 FOR J=1 TO M:AZ(I,J)=HESSE(I,J):NEXT J

8730 NEXT I

8740 GOSUB *INVERSE

8750 GOSUB *PROPAGATION

8760 RETURN

8770 '

8780 *D:

8790 DATA 61

8800 DATA 29,103

8810 DATA 29,102

8820 DATA 29,101

8830 DATA 29,100

8840 DATA 29,99

8850 DATA 29,98

8860 DATA 28,97

8870 DATA 28,96

8880 DATA 28,95

8890 DATA 28,94

8900 DATA 27,93

8910 DATA 27,92

8920 DATA 27,91

8930 DATA 26,90

8940 DATA 27,89

8950 DATA 27,88

8960 DATA 26,87

8970 DATA 26,86

8980 DATA 26,85

8990 DATA 26,84

9000 DATA 25,84

9010 DATA 24,83

9020 DATA 23,83

9030 DATA 22,82

9040 DATA 22,81

9050 DATA 22,80

9060 DATA 23,79

9070 DATA 24,79

9080 DATA 25,79

9090 DATA 26,78

9100 DATA 27,78

9110 DATA 28,78

9120 DATA 29,77

9130 DATA 29,78

9140 DATA 30,76

9150 DATA 30,75

9160 DATA 31,74

9170 DATA 31,73

9180 DATA 32,72

9190 DATA 32,71

9200 DATA 33,70

9210 DATA 33,69

9220 DATA 32,68

9230 DATA 31,67

9240 DATA 31,66

9250 DATA 30,66

9260 DATA 29,65

9270 DATA 29,64

9280 DATA 28,63

9290 DATA 28,62

9300 DATA 29,61

9310 DATA 30,60

9320 DATA 29,59

9330 DATA 30,58

9340 DATA 31,57

9350 DATA 32,57

9360 DATA 32,56

9370 DATA 31,55

9380 DATA 31,54

9390 DATA 31,53

9400 DATA 31,52

　

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　

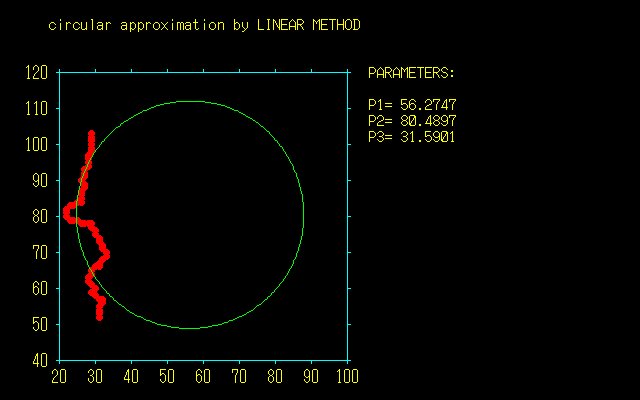
［２］線形最小２乗法の計算結果

　

　このプログラムでは，パラメータｘ0，ｙ0，ｒの誤差を求めるために，線形計算→非線形計算をしているのであるが，ｘ0，ｙ0，ｒの値だけなら線形計算だけでも可能である．1080行を非実行文

　　1080 'GOSUB *EXECUTION:L2$="GAUSS-NEWTON METHOD"

として，線形計算の結果を調べてみることにした．なお，その際，パラメータの誤差は非線形計算のサブルーチンを利用して求めている（8640〜8760行）．

　

　まず最初に，モデル式を

　　ｆ（ｘ，ｙ）＝ａ1（ｘ^2＋ｙ^2）＋ａ2ｘ＋ａ3ｙ−１

と設定した（モデル式１）．この定式化は不自然のように思われるかもしれないが，それは（その３）のプログラムを円のあてはめ用に書き換えるのに，書き換えが最小限で済むようにしたためである．

　

　そのあとで，

　　ａ1，ａ2，ａ3　→　ｘ0，ｙ0，ｒ

の変換式を利用すると，

　　ｘ0＝５６．２７±．６５

　　ｙ0＝８０．４９±．１３

　　ｒ ＝３１．５９±．５８

が得られた（パラメータ・セット１）．

　

　

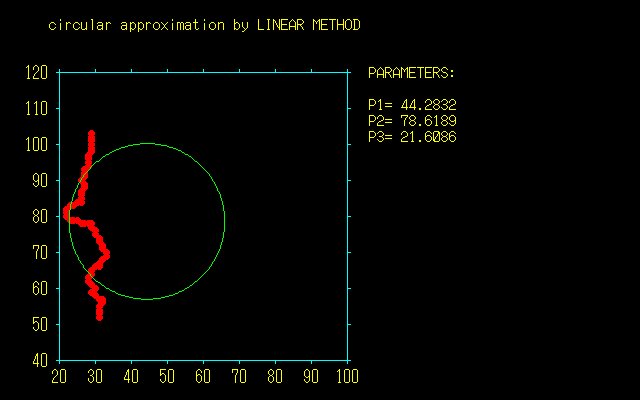
　ところが，モデル式として

　　ｆ（ｘ，ｙ）＝ｘ^2＋ｙ^2＋ａ1ｘ＋ａ2ｙ＋ａ3

（モデル式２）を採用したところ，結果は，

　　ｘ0＝４４．２８±．２４

　　ｙ0＝７８．６２±．１１

　　ｒ ＝２１．６１±．１７

であった（パラメータ・セット２）．

　

　

　同じ円であっても定式化の違いによって，パラメータの推定値にかなりの違いを生ずることがわかったわけであるが，モデル式によってこれほど大きな差がでるとは予想外のことであった．

　

　モデルの定式化によって得られる近似が異なるのでは，実用上困るわけであるが，どちらかが間違いという問題ではなくて，線形最小２乗法的にはどちらも正しいのである．この原因は，データの誤差が小さいときは線形最小２乗法でも準最適解が得られるのだが，データの誤差が大きいときはモデル式によって測定値の誤差が過大評価されたり過小評価されたりすることになり，求めた値には偏りが生じるためと考えられる．

　

　すなわち，背後でデータの質の悪さが影響しているため，モデルの選び方によってデータに対する重みづけが大きく変わってくることが原因となっているのである．線形法の限界と思われた．

　

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　

［３］非線形最小２乗法の計算結果

　

　この問題を解決するには，非線形法による近似が考えられる．そこで，線形法で得られた２通りのパラメータ・セット１，２を初期値として用いて非線形最小２乗法を行ってみた．

　

　その際，モデル式３

　　ｆ（ｘ，ｙ）＝（（ｘ−ｘ0）／ｒ）^2＋（（ｙ−ｙ0）／ｒ）^2−１

と，スケールの異なるモデル式４

　　ｆ（ｘ，ｙ）＝（ｘ−ｘ0）^2＋（ｙ−ｙ0）−ｒ^2

の２つのモデル式を使って，４通りの組合せで比較した．モデル式３はモデル式１に，モデル式４はモデル式２に本質的に等価である．

　

　モデル式３に対する非線形最小２乗法（ガウス・ニュートン法）ではいずれのパラメータ・セットを用いても収束しなかった．シンプレックス法などは試みなかったが，ガウス・ニュートン法では発散したということはサンプルデータのたちが悪いことに加えて，モデル式３に問題があることを示唆している．モデル式の選び方に対しては敏感であり，非線形最小２乗法といえども万能ではないことがわかった．

　

　その点，モデル式４

　　ｆ（ｘ，ｙ）＝（ｘ−ｘ0）^2＋（ｙ−ｙ0）−ｒ^2

の場合は両方のパラメータ・セットで収束し，いずれも

　　ｘ0＝４４．２８±．６１

　　ｙ0＝７８．６２±．１２

　　ｒ ＝２１．６１±．４６

となった．

　

　線形法では２つのあてはめ結果がかなり異なるものになったが，近似がよくないなりにモデル式２，すなわち，

　　ｆ（ｘ，ｙ）＝ｘ^2＋ｙ^2＋ａ1ｘ＋ａ2ｙ＋ａ3

に対して線形最小２乗法を適用して得られた値（パラメータセット２）

　　ｘ0＝４４．２８±．２４

　　ｙ0＝７８．６２±．１１

　　ｒ ＝２１．６１±．１７

の方が良くあてはまっていた．

　

　この値はモデル式４

　　ｆ（ｘ，ｙ）＝（ｘ−ｘ0）^2＋（ｙ−ｙ0）−ｒ^2

を用いた非線形法の最終収束値にほぼ一致した値であることがわかったが，これはモデル式２とモデル式４が本質的に等価であることを裏付けるものである．

　

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　

［４］計算結果のまとめ

　

　以上の結果より，モデルの定式化によって得られる近似が異なることがわかった．データの問題はさておき，近似に影響する要素は以下のように考えられる．

　

１．モデルの定式化

　　(a)ｆ（ｘ，ｙ）＝ａ1（ｘ^2＋ｙ^2）＋ａ2ｘ＋ａ3ｙ−１

　　(b)ｆ（ｘ，ｙ）＝ｘ^2＋ｙ^2＋ａ1ｘ＋ａ2ｙ＋ａ3

　　(c)ｆ（ｘ，ｙ）＝（（ｘ−ｘ0）／ｒ）^2＋（（ｙ−ｙ0）／ｒ）^2−１

　　(d)ｆ（ｘ，ｙ）＝（ｘ−ｘ0）^2＋（ｙ−ｙ0）−ｒ^2

　

２．フィッティング法

　　(a)線形法

　　(b)非線形法（Gauss-Newton，Newton法など）

　　(c)粟屋の２次元フィッティング法

　

　当初，円の近似にはフィッティング法がモデル式の選び方より大きく影響すると思われたのだが，モデル式の影響が大きいということは予想外であった．しかし，モデル式に問題があるのか，使っているフィッティング方法に問題があるかを一般的には判断することは難しい問題であろう．よくあてはまるかどうかの本質な問題はサンプルデータにあると考えられるからである．

　

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　

［５］粟屋の２次元フィッティング法

　

　今回のコラムで取り上げた円近似は（ｘ，ｙ，ｚ）空間の回転放物面

　　ｚ＝（ｘ−ｘ0）^2＋（ｙ−ｙ0）^2−ｒ^2

を想定して，ｚ軸方向の残差２乗和

　　Σ｛ｚ−ｆ（ｘ，ｙ）｝^2

が最小となるような回転放物面を求めるものである．この回転放物面の（ｘ，ｙ）平面での切り口が円になっているというわけである．

　

　この項では，これまで検討してこなかった粟屋の２次元フィッティング法を取り上げることにする．残差２乗和の取り方にはいろいろ考えられるが，測定点からあてはめるべき円に下ろした垂線の長さ（データから円までの最短距離）

　　ｓ＝√｛（ｘ−ｘ0）^2 ＋（ｙ−ｙ0）^2｝−ｒ

の平方和Σｓ^2が最小になるように定めることも可能である．

　

　もちろん，残差２乗和の取り方によりあてはめ結果は当然違ってくるが，そのような方法に，粟屋の２次元フィッティング法がある．粟屋の方法を一言でいうならば，陽関数におけるガウス・ニュートン法を陰関数まで取り扱いを拡張したものであって，線形関数・非線形関数いずれの場合もユニバーサルに取り扱うことができる方法ということになろう．粟屋の方法については（その１）に概略を記したので，それを参照して頂きたい．

　

　最小２乗法ソフト「耕太郎」にサポートされている粟屋の方法，すなわち，垂線の長さの平方和を最小にするあてはめ結果を掲げると

　　ｘ0＝１１８．７５±３．１３

　　ｙ0＝　８５．５８±０．３７

　　ｒ ＝　９１．９６±３．１１

となった．円の場合，粟屋の方法を適用することは楕円の場合よりもかなり楽になるものと思われるが，それについては機会を改めて述べることにしたい．

　

　なお，今回掲げたプログラムの

2690　 E1(I)=Y1(I)-YH

2700　'E1(I)=SQR((X(1)-P(1))^2+(X(2)-P(2))^2)-ABS(P(3))

を

2690　'E1(I)=Y1(I)-YH

2700　 E1(I)=SQR((X(1)-P(1))^2+(X(2)-P(2))^2)-ABS(P(3))

に，

3430　 SS=SS+WT(K)*(Y1(K)-YH)^2

3440　'E1(K)=SQR((X(1)-P(1))^2+(X(2)-P(2))^2)-ABS(P(3))

3450　'SS=SS+WT(K)*(E1(K))^2

を

3430　'SS=SS+WT(K)*(Y1(K)-YH)^2

3440　 E1(K)=SQR((X(1)-P(1))^2+(X(2)-P(2))^2)-ABS(P(3))

3450　 SS=SS+WT(K)*(E1(K))^2

に書き換えると，粟屋の方法を擬似体験することができる．

　

　（その１）で述べたように粟屋の方法は変数が多くなるため，実用的ではない．この変更は速く収束することを期待した粟屋の方法の簡易版というわけであるが，実行してみると，ガウス・ニュートン法にしてはゆっくりとした収束で２次収束は期待できそうになかった．

　

　また，デフォルトの収束判定条件での最終収束値は

　　ｘ0＝６４．０１±０．１１

　　ｙ0＝７９．１２±０．００

　　ｒ ＝４０．２８±０．０１

となったが，これは局所的な極小値で計算が停止したものであって，信頼できる値ではない．以上のように，粟屋の方法の簡易版は期待はずれで，やはり本家・本元にはかなわないものと思われた．

　

［参］粟屋隆「データ解析」学会出版センター

　

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝