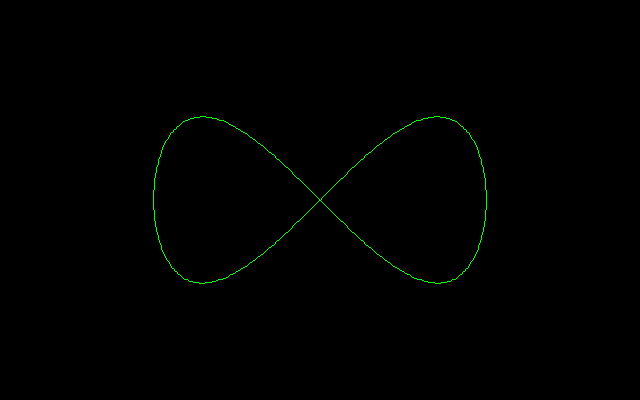
つい最近,
[参]礒田正美編「曲線の事典」,共立出版
が刊行されました.曲線の事典というよりは「リンク装置」(複数の棒を互いに結合してできる連接棒の一点を直線や曲線に沿って動かすとき,複雑な変化のある曲線を描くことができる)の事典であり,リンク装置についてのおもしろい記事が満載された大部です.リンク装置の用途は多方面にわたり,角の3等分問題や立方体倍積問題を解くのにも使われます.
ありがたいことに,この本は大部であるにも関わらず破格の廉価(3800円)です.そのカラクリはインターネット上の記事を元にして編集されているからのようです.今回のコラムでは
[参]礒田正美編「曲線の事典」,共立出版
の助けを借りて,コラム「代数幾何学小話」を補完しておきたいと思います.
なお,当該書籍でリンク装置の性質・歴史・作図法に関心をもたれた読者は
[参]ドメイン&オルーク「幾何的な折りアルゴリズム」上原隆平訳,近代科学社
にステップアップすることをお勧めします.
===================================
【1】代数曲線と代数曲面
18,19世紀になると,2次曲線論に続いて3次および4次曲線について論じられた.3次曲線の分類には,2次曲線とは異なった種類の難解さが要求されたが,ニュートンはあらゆる場合を考察して,最終的に3次曲線は全部で78種類が必要であることを示すに至り,さらに3次曲線の一般式が5個の標準形に帰することを示した.
[補]ニュートンは係数の値によってとりうる3次曲線の形を72種類挙げた.しかし,実際には78種類あり,残り6種類のうち4種類はスターリング,2種類はニコルとベルヌーイが発見している.
[補]代数幾何学において重要な変換に双有理変換(クレモナ変換)があるが,ニュートンは楕円,放物線,双曲線から3次曲線を得るのに双有理変換を使っている.この例からわかるように代数曲線の次数は双有理変換で不変ではないが,種数は不変である.すなわち,ニュートンは代数操作という変換を用いており,78種類というのは(幾何学的な分類ではなく)代数的な分類となっている.プリュカーは幾何学的な分類方法によって3次曲線を219種に分類している(1835年).
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
ニュートンの3次曲線の分類に引き続いて,オイラーは4次平面曲線の分類を企てたが,可能な場合の数が非常に多いという理由で断念している.この問題に対する答えは長い間知られていなかったが,プリュッカーが19世紀に4次曲線の152の型を数え上げることによって解かれた.プリュッカーはオイラーが4次曲線の分類で犯した多くの誤りを見つけたが,18世紀の解析幾何とは違って,高次曲線,曲面は解析幾何の対象ではなく,代数幾何の分野となった.
1849年,ケーリーは滑らかな3次曲面はすべてある一定数の直線を含むこと,サーモンはその数は27であることを証明した.1次曲面(平面)は∞^2個,2次曲面は∞^1個の直線を含み,一般の3次曲面では(少なくとも1本の直線を含むが)その数は高々有限個(27本)である.それに対して,一般のn次曲面(n>3)は直線を全然含んでいない.
シュレーフリは3次曲面上の27本の直線の組に従って,滑らかな実3次曲面を5組に分類した.この5組にはそれぞれ27,15,7,3,3本の実直線,そして3直線を含む実平面が45,15,5,7,13入っている.
アルキメデスの墓石に円柱・円錐・球,ガウスの墓石に正17角形が彫られた如く,ケーリーとサーモンの墓石には27本の直線を彫るべきだとシルベスターがいったことは19世紀にこれらの3次曲線がいかに重要視されたかを物語るものだろう.
===================================
【2】ギリシャの3大作図不能問題
与えられた条件を満足する図形を作図するのに用具を定規とコンパスに限るのは古代ギリシャ以来の伝統です.定規とコンパスだけで
a)与えられた角を三等分すること(角の3等分問題)
b)立方体の二倍の体積をもつ立方体の一辺を作図すること(立方体倍積問題)
c)円と等積な正方形を作図すること(円の正方形化問題・円積問題)
これらの3つの問題はギリシャの3大作図問題として有名なものですが,実は19世紀になってから作図不能であることが証明されています.
正方形の対角線を1辺とする正方形の面積は最初の正方形の2倍であることは明白です.したがって,正方形の2倍の面積の正方形を求める作図問題は簡単に解くことができます.そこで,次なる問題は立方体の2倍の体積をもつ立方体を求めることです.別名デロスの神殿問題と呼ばれるこの問題も簡単に解けるに違いないと思ったのでしょうが,1辺の長さが2倍の立方体の体積はもとの立方体の2^3倍の体積,立方体の対角線を1辺とする立方体は3^3/2倍の体積になってしまい,簡単には求まりません.
また,角を2等分したり,特殊な角の3等分問題,たとえば,180°,90°,45°などに対しては角を3等分する問題はまったく簡単に解くことができます.直角の倍角,半角ような特殊な角を3等分するのはわけのないことですから,角の3等分問題では任意の角を3等分する作図法を問題にします.
無限等比級数
1/3=1/2^2+1/2^4+1/2^6+1/2^8+・・・
より,角の2等分を無限回繰り返すことによって角の3等分が可能になることが理解されます.しかし,ここでは有限回の操作だけに限ることにして,また,たまたまある角度に対してとかコンコイドやシッソイドなど特殊な曲線を描くための定規は禁じ手とします.
立方体倍積問題,角の3等分問題,円の正方形化問題(円積問題)のいずれの幾何学的問題も代数方程式に対応していて,たとえば,倍積問題はx^3−2=0,角の3等分問題はx^3−3x−a=0,円積問題はx^2−π=0に帰着します.
定規とコンパスで描ける図形は直線と円ですから,その作図は線分の長さの加減乗除と平方根をとる操作に相当します.すなわち,定規(直線)とコンパス(円)による作図は,たとえそれらを繰り返し用いたとしても,+,−,×,÷,√なる5つの演算によって得られるものに限られています.
したがって,倍積問題のように3次方程式に帰着する作図問題は+−×÷√の演算を組み合わせても解けません.角の3等分問題は,aの値によっては定規とコンパスのみで3等分できる角が無数にあると同時に,3等分できない角もまた無数にあることを示しています(ワンツェル).モーリーの定理「任意の三角形において,各内角の3等分線の隣同士の交点を結んで得られる三角形は正三角形である.」この驚くべき定理が20世紀にいたるまで発見されなかった理由も,角の3等分問題は解けないことが判明していたところにあるのでしょう.また,円積問題は2次方程式に帰着しますが,√πがコンパスと定規で作図できたとすると,その平方であるπも同様に作図可能ということになります.しかし,πは超越数ですから√πも超越数なのです.したがって,√πは代数方程式の解とはなりえず,円積問題も作図不能となるのです(リンデマン).
−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−
[補]コンコイド・シッソイド
ギリシア人は新しい数学曲線を見いだして立方体倍積問題や角の3等分問題などを解決しました.60°,30°,15°など任意の角の場合でも,定規とコンパスというプラトンの束縛から離れて,コンコイドやシッソイドという曲線の性質を用いた適当な道具を使えば作図可能となります.
<ニコメデスのコンコイド>
定点Oと定直線gが与えられているとき,Oを通る任意の直線とgとの交点をQとし,この直線上にQから定距離lの点Pをとると,この点Pの軌跡をコンコイドといいます.
極座標ではr=a/cosθ+b
x,y座標で書けば,x=a+bcosθ,y=atanθ+bsinθ
θを消去すると,4次曲線:
(x^2+y^2)(y−a)^2=b^2y^2
(x−a)^2(x^2+y^2)=l^2x^2
で表されます.なお,直線に関するコンコイドがニコメデスのコンコイドであって,円の関するコンコイドがリマソンであり,カーディオイドはその特殊な場合となっています.
<ディオクレスのシッソイド>
r=a/cosθ−acosθ
x=asin2 θ,y=asin^2θ・tanθ
θを消去すると3次曲線:x(x^2+y^2)=ay^2が得られます.
===================================
【3】直角定木とコンパスによる作図不可能問題の作図
定木とコンパスに限定すると作図できないことがワンツェルやリンデマンによって証明されたわけですが,1931年,ビーベルバッハは「直角」定木とコンパスを使って
a)与えられた角を三等分すること(角の3等分問題)
b)立方体の二倍の体積をもつ立方体の一辺を作図すること(立方体倍積問題)
を解き,さらに3次方程式と4次方程式で表される作図問題がすべて解けることを示しました.
===================================
【4】レムニスケート
レムニスケートといえば,一般にベルヌーイのレムニスケートを指す場合が多いが,もともと8の字曲線を表す用語であり,Geronoのレムニスケート,Boothのレムニスケート,Montferrierのレムニスケート,Slueseのレムニスケートなど多くのレムニスケートがあるそうだ.Geronoのレムニスケート:(x,y)=(cosθ,sinθcosθ)はリサージュ曲線の1つとして知られている.
コラム「楕円積分の加法定理(その8)」において,『ベルヌーイのレムニスケートは三角関数を用いて
x=cosθ/(1+sin^2θ)
y=sinθcosθ/(1+sin^2θ)
とパラメトライズされるが,阪本氏によるとGegoroのレムニスケート
x=sinθ
y=sinθcosθ
というのもあるそうだ.以下にGegoroの連珠形を掲げる.
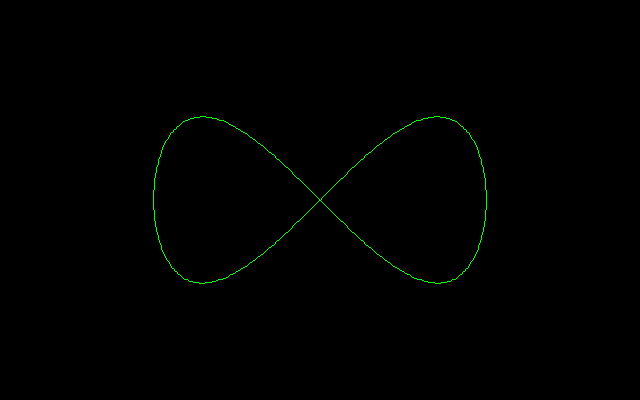
』と記したが,阪本氏が
[参]グレイ「曲線と曲面の微分幾何」小島順監訳,竹沢護訳,トッパンを参考にした際にスペルミスしたもので,Geronoが正しい.
===================================