【１】面積７倍の三角形

　三角形の３辺をそれぞれ２倍の長さになるまで延長する．その面積は元の三角形の７倍である．このことは，図にいくつかの補助線を引いてやれば，面積は等しい７つの三角形ができることから示される．

　一般に与えられた三角形の各辺を同じ倍率ｋで伸縮した位置に点をとって作った三角形の面積は，もとの三角形の面積の

　　Ｍ＝３ｋ^2−３ｋ＋１＝３（ｋ−１／２）^2＋１／４

倍になる．

　　ｋ＝１／３　→　Ｍ＝１／３　　（３等分）

　　ｋ＝１／２　→　Ｍ＝１／４　　（４等分）

　　ｋ＝２／３　→　Ｍ＝１／３　　（３等分）

　　ｋ＝１　　　→　Ｍ＝１

　　ｋ＝２　　　→　Ｍ＝７　　　　（７等分）

となる．

　０＜ｋ＜１のときはもとの三角形より小さくなり，ｋ＝１／２のとき最小値１／４をとる．ｋ＞１のときはもとの三角形より大きくなり，ｋ＝２のときには７倍になる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】縮小三角形

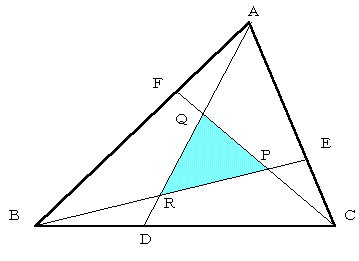
　三角形ＡＢＣの各辺を１：λの比に順次内分した点Ｄ，Ｅ，Ｆとし，ＡＤ，ＢＥ，ＣＦの２本ずつの交点が作る三角計ＰＱＲを仮に「縮小三角形」と呼ぶことにする．

　一般に，与えられた三角形の各辺をλ：１，μ：１，ν：１に分ける位置に点をとって対頂点と結んで作った三角形の面積は，もとの三角形の面積の

　　Ｍ＝（λμν−１）^2／（λμ＋λ＋１）（μν＋μ＋１）（νλ＋ν＋１）

倍に等しくなる．

　この場合はλ＝μ＝νであるから，

　　Ｍ＝（λ^3−１）^2／（λ^2＋λ＋１）^3

＝（λ−１）^2／（λ^2＋λ＋１）

λ＝１（中線）のとき，三角形は重心に退化するというわけである．

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

　ここでは各辺をλ：１に内分する位置にとったが，パラメータを変えて，各辺をδ：１−δ　　（０＜δ＜１／２）に内分する位置にとると，

　　λ＝δ／（１−δ）

　　Ｍ＝（１−２δ）^2／（１−δ＋δ^2）

となる．

　なお，与えられた三角形の各辺をλ：１，μ：１，ν：１に分ける位置に点をとって点同士を結んで作った三角形の面積は，もとの三角形の面積の

　　Ｍ＝（λμν＋１）／（λ＋１）（μ＋１）（ν＋１）

倍に等しくなる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝