今回のコラムでは凧型多面体に黄金化・白銀化を施してみます．菱形多面体の黄金化・白銀化では菱形面を２等分するには方法には長い方の対角線で２等分するものと短い方の対角線で２等分するものの２通りありましたが，凧型多面体の場合は長い方の対角線で２等分するしかありません．凧型二十四面体の黄金化により六方八面体の亜種，凧型６０面体の白銀化により六方二十面体の亜種ができあがります．

　金原博昭さんのお話ですと，凧型二十四面体の黄金化によって閉じた４８面体ができるとのことでしたが，（その１）で行った計量から閉じた多面体になることはほとんどあり得ないと考えられました．閉じるとしたらそれは紙模型の工作誤差と思われるのですが，今回のコラムではそのことについて検証してみます．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】閉じた多面体になるための条件

　凧型２４面体の黄金化多面体が閉じた多面体になるための条件は，ｋ≦１として，４つの頂点の座標が

　　Ａ（０，０，７−４√２）

　　Ｂ（（−８＋７√２）ｋ／２，０，（−８＋７√２）ｋ／２）

　　Ｃ（０，（−８＋７√２）ｋ／２，（−８＋７√２）ｋ／２）

　　Ｄ（（−９＋１０√２）／７，（−９＋１０√２）／７，（−９＋１０√２）／７）

になることです．

　同様に，凧型６０面体の白銀化多面体が閉じた多面体になるための条件は，ｋ≧１として，４つの頂点の座標が

　　Ａ（０，０，（９φ＋１３）／１８）

　　Ｂ（（６φ−５）ｋ／６，０，（φ＋６）ｋ／６）

　　Ｃ（（６φ−５）ｋ／６０ｃｏｓ７２°，（６φ−５）ｋ／６０ｓｉｎ７２°，（φ＋６）ｋ／６）

　　Ｄ（（１７φ＋２０）／６６，（１７φ＋２０）／６６ｔａｎ３６°，（３７φ＋１７）／６６）

になることです．

　ｋの値を変えたとき，ＡＢ／ＡＤと∠ＢＡＤがどのように変化するかを調べてみました．

［１］ＡＢ／ＡＤ

［２］∠ＢＡＤ

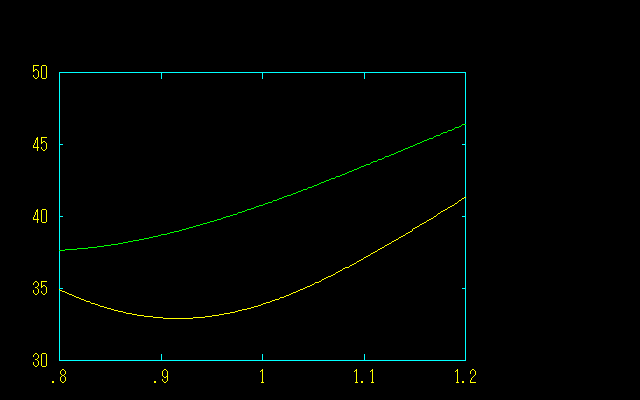
　凧型２４面体（緑），凧型６０面体（黄）のグラフを描いてみると，∠ＢＡＤ=33.8915のグラフには交点がないことがわかります．一方，∠ＢＡＤ=40.7895のグラフに交点が出現することがわかります．これは凧型２４面体の黄金化は不可能，凧型６０面体の白銀化は可能であることを意味しています．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】二面角関数

　菱形多面体では二面角関数は簡単な形に表せました．それに対して，凧型多面体では簡単な形にはならないので，数値的に二面角δの変化を調べてみることにしました．

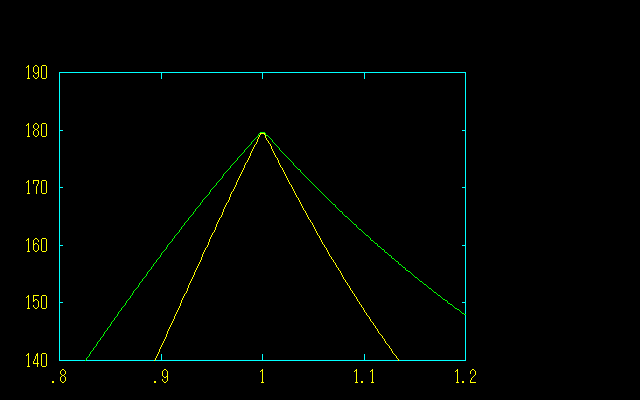
　二面角が補角となる多面体が存在することは明らかですが，黄金凧型と白銀凧型は相互補完的な関係にはないのです．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝