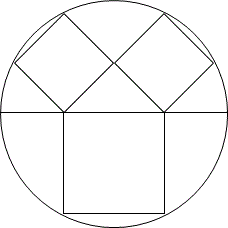
（その３３）に掲げた下図は，黄金分割の別法になっている．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】黄金分割の別法（１）

　半径１の単位円に内接する正三角形を考える．

　　Ａ（１，０）

　　Ｂ（−１／２，√３／２）

　　Ｃ（−１／２，−√３／２）

　ＡＢ，ＡＣの中点

　　Ｍ（１／４，√３／４）

　　Ｎ（１／４，−√３／４）

を通る直線：ｘ＝１／４と単位円との交点は

　　（１／４）^2＋ｙ^2＝１→Ｌ（１／４，√１５／４）

　ＭＮ＝√３／２

　ＬＮ＝（√３＋√１５）／４

したがって，ＬＮ／ＭＮ＝（１＋√５）／２＝φ

すなわち，黄金分割の別法である．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】黄金分割の別法（２）

　半径１の単位円の半円を考える．直径上に接点をもつ円（半径ｒ）を３個を内接させる．３円の中心は

　　Ａ（−２ｒ，ｒ）

　　Ｂ（０，ｒ））

　　Ｃ（２ｒ，ｒ）

　　ｒ√５＋ｒ＝１

　　ｒ＝１／（１＋√５）

　したがって，大きい半円の半径を小さい円の直径で割ると

　　１／２ｒ＝（１＋√５）／２＝φ

すなわち，黄金分割の別法である．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝