ルーローの三角形を正方形の内で回転させるドリルは４隅が少し丸みを帯びていましたが、このドリルはピッタリ90度になります。

1ヶ月位前にアメリ他のStan Wagonからメールが届き、彼が発想を換えて、直角二等辺三角形Tを基に定幅図形を作り、その図形内の点（Tの直角頂点）の位置に刃を埋め込んだものです。最近、その回転ドリルの模型を製作したので、その映像を送ります。

※映像は下記リンク先からDLをお願いします。　　（秋山仁）

https://tus.box.com/s/m229qqun1tuv7ch2rsbpksibk1oulc38

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

この論文は

Barry Cox, Stan Wagon

Drilling of Polygons

American Math Monthly, 300- 312, 2012 にあります

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

この図形内の点Oが正方形を描くのである

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

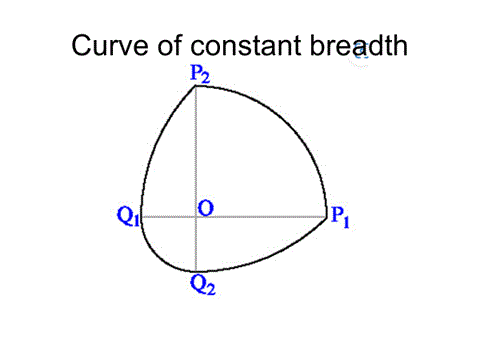
P1(√2,0,0)

P2(0,√2,0)

P3(0,0,√2,0)

Q1(√2-2,0,0)

Q2(0,√2-2,0)

Q3(0,0,√2-2)

円弧P1P2:中心O,半径√2

円弧P2Q1:中心P1,半径2

円弧Q1Q2:中心O,半径2-√2

円弧Q2P1:中心P2,半径2

√2-(2-√2)=2√2-2~）＝ru-toru-to

P1P2を下にして転がすと点Oの高さ=√2は一定に保たれる

Q1Q2を下にして転がすと点Oの高さ=2-√2は一定に保たれる

1辺の長さ2の正方形の中に、1辺の長さ√2-(2-√2)=2(√2-1)の正方形を描くことになる

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

P2Q1を下にして転がすと点Oと接点との距離は一定に保たれない

このとき、P1P2、Q1Q2は側壁にあり、側壁からの距離が一定に保たれる→真四角の穴を開けることができる

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝