円の接線極座標における方程式は
p(θ)=a0/2+a1cosθ+b1sinθ
で与えられます.
p(θ)+p(θ+π)=a0
ですから定幅曲線で,その曲率半径はa0/2となります.
ルーローの三角形は定幅曲線ですが,ルーローの三角形の平行曲線もまた定幅曲線です.それではルーローの三角形ではなく,デルトイドの平行曲線は定幅曲線になるでしょうか?
===================================
【1】デルトイドの平行曲線
デルトイド
ξ=a(2cosθ+cos2θ)=2acosθ(1+cosθ)−a
η=a(2sinθ−sin2θ)=2asinθ(1−cosθ)
において,
dε/dθ=−a(2sinθ+2sin2θ)=−2asinθ(1+2cosθ)
dη/dθ=a(2cosθ−2cos2θ)=2a(1−cosθ)(1+2cosθ)
(dε/dθ)^2+(dη/dθ)^2=8a^2(1−cos3θ)=8a^2(1+2cosθ)^2(1−cosθ)=16a^2(1+2cosθ)^2sin^2(θ/2)
ですから,平行曲線は
x=2acosθ(1+cosθ)−a+rsin(θ/2)
y=2asinθ(1−cosθ)+rcos(θ/2)
および
x=2acosθ(1+cosθ)−a−rsin(θ/2)
y=2asinθ(1−cosθ)−rcos(θ/2)
のようになります.
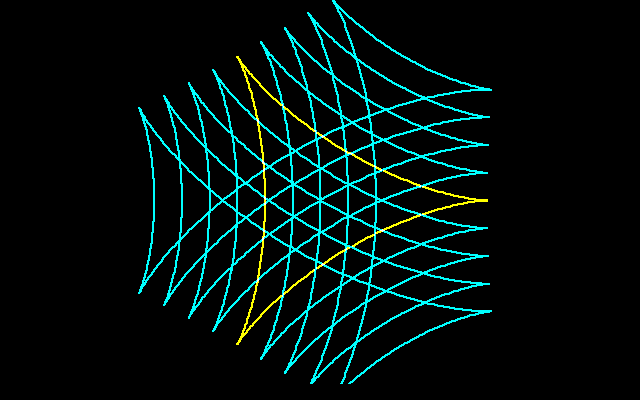
a=1,r=0.5〜2の範囲で図示すると,6つのカスプをもつ曲線が描かれます.6つの尖点はデルトイドの平行曲線の特異点です.

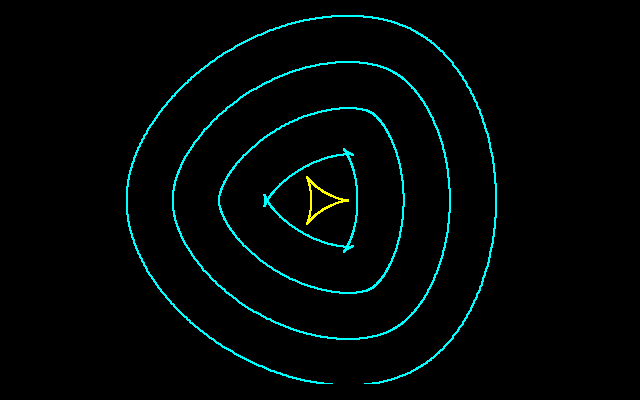
a=1,r=5〜20の範囲で図示すると,r=10では特異点が解消されていることがわかります.これは定幅曲線となるのでしょうか?
===================================
【2】接線極座標と内転形
計算の都合上,デルトイドの平行曲線の方程式を
x=2acosθ(1+cosθ)−a+rsin(θ/2)
y=−2asinθ(1−cosθ)−rcos(θ/2)
とおいて
xsinθ−ycosθ=p(θ)
に代入すると,包絡線の接線極座標における方程式は
p(θ)=2asin2θ−asinθ+rcos(θ/2)
で与えられます.
p(θ)+p(θ+π)≠(一定)
ですから,デルトイドの平行曲線は定幅曲線ではありません.
===================================
【3】訂正
[参]「東北大学数学教室の歴史」
には『フルヴィッツはフーリエ級数論を応用して「デルトイドの平行曲線が定幅曲線(平行な支持線間の距離が一定な卵形線)である」ことを証明した』という意味のことが書かれています.
それを受けて(信じて)
コラム「デルトイドの幾何学(その8・藤原と掛谷)」
コラム「デルトイドの幾何学(その9)」
などに引用したのですが,
「デルトイドの平行曲線は正方形の内転形である」
はどうやら間違いであって,
「アステロイドの平行曲線は正三角形の内転形である」
が正しいようです.
ともあれ,この論文から刺激をうけた藤原松三郎は,一般的な凸多角形の内転形をフーリエ級数論
p(θ)=a0/2+Σ(akcoskθ+bksinkθ)
を応用して解析的に研究しました.
[1]同じ凸多角形のすべての内転形の周長は等しい
[2]正n角形の内転形は少なくとも2(n−1)個の頂点をもつ
などはその業績の一例です.
===================================
【補】平行曲線
中心の軌跡が(ξ(θ),η(θ))でパラメータ表示される半径rの円
(x−ξ(θ))^2+(y−η(θ))^2=r^2
y=η(θ)±{r^2−(x−ξ(θ))^2}^(1/2)
の一部がドリルの円弧であるとき,
∂y/∂θ=0 → (x−ξ(θ))dξ/dθ+(y−η(θ))dη/dθ=0
これより,包絡線の方程式は
x=ξ(θ)+rdη/dθ/{(dξ/dθ)^2+(dη/dθ)^2}^(1/2)
y=η(θ)−rdξ/dθ/{(dη/dθ)^2+(dξ/dθ)^2}^(1/2)
および
x=ξ(θ)−rdη/dθ/{(dξ/dθ)^2+(dη/dθ)^2}^(1/2)
y=η(θ)+rdξ/dθ/{(dη/dθ)^2+(dξ/dθ)^2}^(1/2)
とパラメータ表示されます.
これは中心の軌跡(ξ,η)と直交する方向(法線方向)にrだけ離れた2点の軌跡です.すなわち,中心の軌跡の平行曲線を描くというわけです.
例をあげると,楕円:x^2/a^2+y^2/b^2=1
のパラメータ表示
ξ=acosθ,η=bsinθ
については
x=acosθ+rbcosθ/(a^2sin^2θ+b^2cos^2θ)^(1/2)
y=bsinθ+rasinθ/(a^2sin^2θ+b^2cos^2θ)^(1/2)
および
x=acosθ−rbcosθ/(a^2sin^2θ+b^2cos^2θ)^(1/2)
y=bsinθ−rasinθ/(a^2sin^2θ+b^2cos^2θ)^(1/2)
のようになります.
===================================