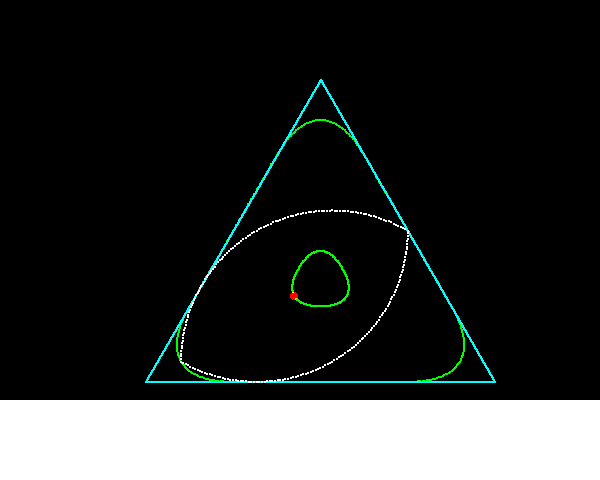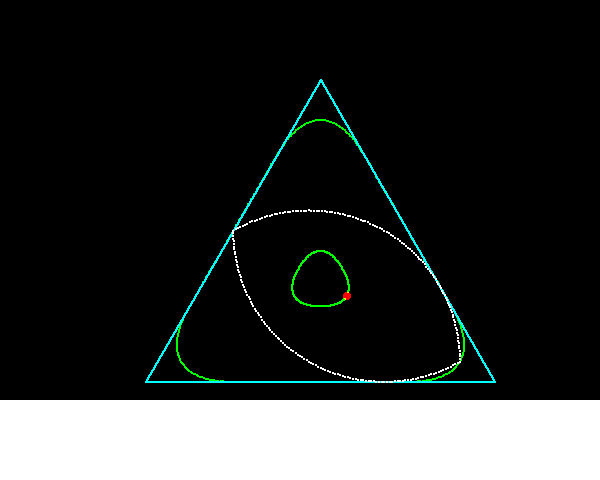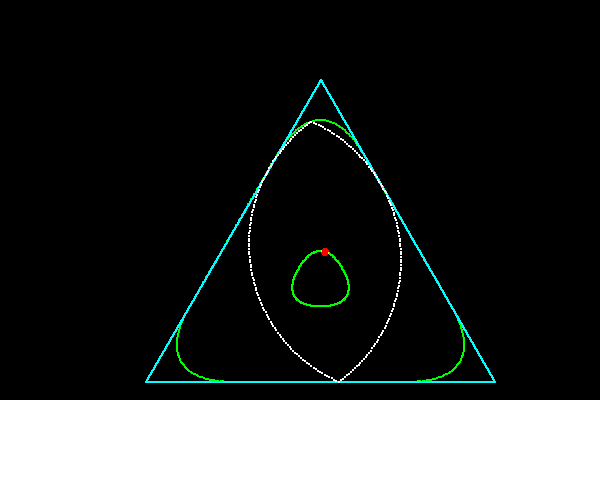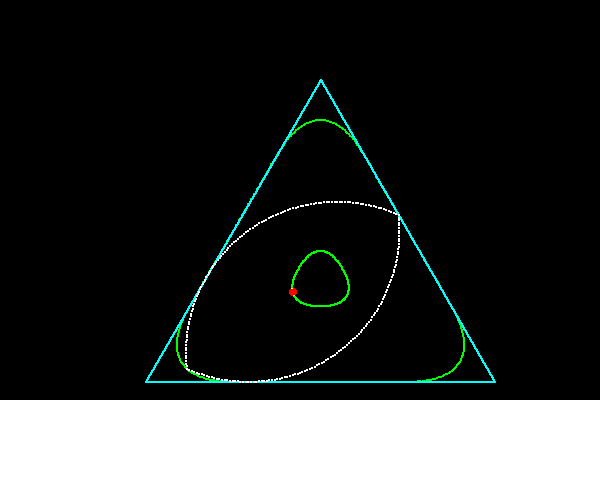
正３角形に内接しながら回転することできる凸閉曲線が，円以外にも存在します．このような図形の一例が，藤原・掛谷の２角形（正三角形の中線を一辺とする正三角形の頂点を中心として，中線の長さを半径とする２個の円弧からなる曲線）で，この性質をもつ曲線の中で囲む面積が最小のものは藤原・掛谷の２角形であることが証明されています．

　藤原・掛谷の二角形は正三角形の高さをｈとすると，半径がｈの円弧を２個組み合わせた頂角６０°の円弧二角形ですから，この図形を応用すれば正３角形の穴をあけるドリルを作ることが可能になります．

　それに対して「ルーローの二角形」は半径がｈ／２の円弧を２個組み合わせた頂角１２０°の太った円弧二角形ですから，正三角形の隅々まで穴をあけることのできません．今回のコラムでは，ルーローの二角形の動画プログラムを組んでみました．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】（その１５）に対応

　藤原・掛谷の二角形は頂角６０°，頂点間距離ｈなので，正三角形の角にすっぽりはまりこみ正三角形の隅々まで穴をあけることができますが，ルーローの二角形（頂角１２０°，頂点間距離√３ｈ／２）ではそれができません．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】（その１４）に対応

　（その１４）に対応する包絡線も描こうとしたのですが，どういうわけか描けませんでした．同じプログラムを使って，藤原・掛谷の二角形やルーローの三角形の場合の包絡線は描けるので，これはルーローの二角形の特殊事情に負っているのかもしれません．原因については後日報告しますが，それまでの間，暫時オーバーレイを掲げておきます．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝