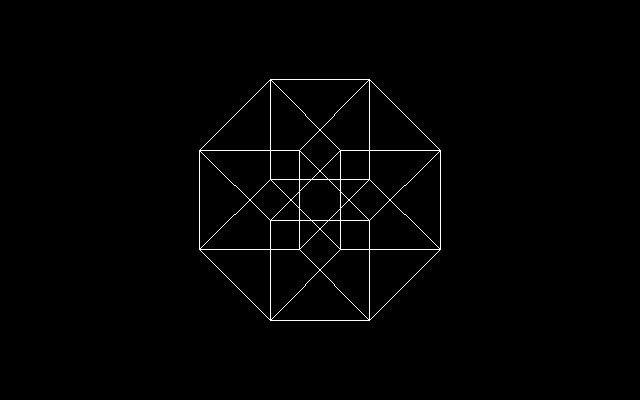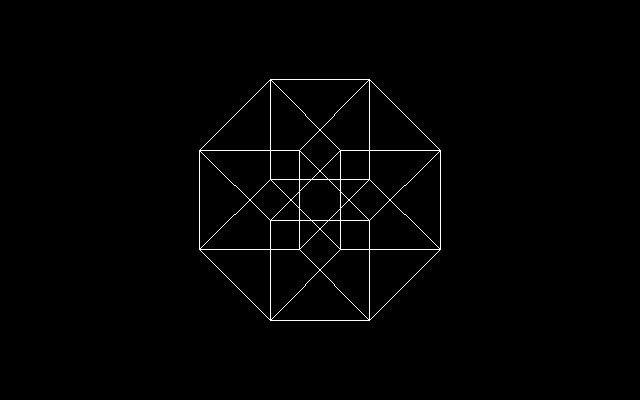石井源久先生の学位論文

　　「多次元半正多胞体のソリッドモデリングに関する研究」

によれば，直交回転行列Ｒの正軸体の変換先は立方体の場合と同じになるという→（その６）（その７）．

　今回のコラムでは，４次元立方体を２次元平面上に複数の頂点がなるべく重ならないように座標軸をとって，実際に描くことを試みたい．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　　Ｒ＝［　１，１／√２，０，−１／√２］

　　　　［　０，１／√２，　１，１／√２］

　　　　［１／２，−１／√２，１／２，０］

　　　　［１／２，０，−１／２，１／√２］

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

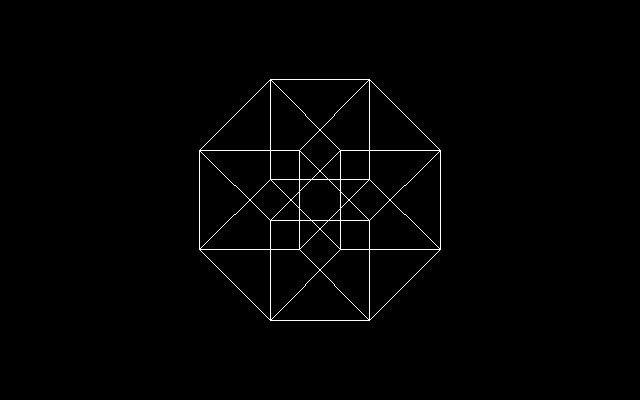
　黄金比は正五角形と密接な関係にある．正五角形に対角線を書き入れると星形五角形できるが，この手順を繰り返すと，正五角形と星形五角形が少しずつ縮小しながら無限に入れ子状になった図形を作ることができる．正五角形に対角線を描き入れると星形五角形（ソロモンの星）ができるが，正五角形と星形五角形の入れ子はペンタグラムと呼ばれる．

　それに対して，白銀比は正八角形と密接な関係にある．正八角形に３／８角形を書き入れると正八角形できるが，この手順を繰り返すと，正八角形と星形８／３角形が少しずつ縮小しながら無限に入れ子状になった図形を作ることができる．ところで，この図形は４次元立方体の３次元投影図でもある．

　ｎ次元立方体を２次元平面上に複数の頂点がなるべく重ならないように座標軸をとることを考える．ｎが２のベキ（ｎ＝２，４，８，１６，・・・）のとき，中止部に穴が開く．ｎが大きくなると，穴はどんどん小さくなる．次は８次元の場合であるが，この辺で止めておこう．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝