シリーズ「切稜立方体」で取り上げた中川宏さんの切稜立方体の木材加工は常にしっかりと面を押しつけられるので安定して作ることができるのですが,それに対して,木を削って「切頂立方体」を作るには切削角度・距離の設定が難しく木工にはむいていません.
しかし,正多面体の頂点を削り落とすと,頂点(v)と面(f)の双対性
v−e+f=2
から,その中間段階でいろいろな準正多面体が得られることがわかります.たとえば,立方体の頂点を次第に削りとると,立方体(cube)→切頂立方体(truncated cube)→立方八面体(cuboctahedron)→切頂八面体(truncated octahedron)→正八面体(octahedron)と移行します.
最終的には立方体の双対多面体である正八面体が得られますが,中間形の切頂立方体,立方八面体,切頂八面体はいずれも準正多面体です.反対に,正八面体の頂点を削っていくと,正八面体→切頂八面体→立方八面体→切頂立方体→立方体ができあがります.一般に,準正多面体は球に外接しませんが内接はします.
切頂八面体は名前のとおり正八面体の各辺を三等分して頂点を切り取った後に残る多面体です.実は,16種類の準正多面体のなかで空間充填が可能なのは切頂八面体−−正6角形8枚と正方形6枚の2種類で作る14面体−−しかありません.切頂八面体は体心立方格子のボロノイ多面体です.
また,立方体の各辺の中点を結んで頂点を切り落とすと,6枚の正方形と8枚の正三角形の合計14面からなる準正多面体ができます.正八面体についても12本の辺の中点を結んでその頂点を切り落とすと全く同じ多面体ができます.このように立方八面体は立方体と正八面体の両方から中点を結ぶという同じプロセスでできあがる準正多面体です.
立方八面体は単独では空間充填形ではありませんが,正八面体と組み合わせると空間充填が可能です.また,立方八面体の双対は菱形十二面体であり,これは単独で空間充填形です.菱形十二面体は面心立方格子のボロノイ多面体となっています.
===================================
さて,p角形面およびq稜頂点をもつ正多面体を,シュレーフリにしたがって
(p,q)
で表すことにしましょう.また,凸多面体の頂点,辺,面の数をそれぞれv,e,fとします.すると,正多面体(p,q),(v,e,f)の切頂正多面体の(V,E,F)は,頂点が正q角形,面が2p角形となり
F=f+v
E=e+qv
V=qv
で表されることがわかります.
今回のコラムでは切頂立方体を計量してみますが,もとの立方体の1辺の長さを2,切頂される頂点から辺までの切削距離をdとおきます(0≦d≦2).すると
d=0:立方体
0<d<1:八角形面6枚と正三角形面8枚からなる14面体
d=1:立方八面体
1<d<2:正方形面6枚と六角形面8枚からなる14面体
d=2:正八面体
で,
d=2−√2
のとき,切頂立方体(正八角形面6枚と正三角形面8枚からなる14面体)
d=3/2
のとき,切頂八面体(正方形面6枚と正六角形面8枚からなる14面体)ができあがります.
以下,これらを総称して広義の切頂立方体,d=2−√2の場合を狭義の切頂立方体と呼ぶことにします.
===================================
【1】0≦d≦1の場合
八角形面の面積:S8=4−2d^2
正三角形面の面積:S3=√3/2d^2
は簡単に求められます.
また,
正三角形面の中心の座標:(1−d/3,1−d/3,1−d/3)
ですから,
原点から八角形面までの距離:H8=1
原点から正三角形面までの距離:H3=√3(1−d/3)
以上により
表面積:S=6S4+8S3
=6(4−2d^2)+4√3d^2
=(4√3−12)d^2+24
体積:V=6S4H4/3+8S3H3/3
=2(4−2d^2)+4d^2(1−d/3)
=−4/3d^3+8
が得られます.
H3=√3(1−d/3)=1
は0≦d≦1の範囲で解をもちませんから,この立体は球に内接するだけで外接しません.なお,狭義の切頂立方体(八角形面が正八角形)となるための条件は
d=2−√2
です.
===================================
【2】1≦d≦2の場合
この場合,正方形面の対角線の長さの半分をrとしてパラメトライズすると,
r=2−d
となります.
正方形面の面積:S4=2r^2=2(2−d)^2
六角形面の面積:S6=√3/2(1+2r−2r^2)
=√3/2(−3+6d−2d^2)
また,
六角形面の中心の座標:(1−d/3,1−d/3,1−d/3)
ですから,
原点から正方形面までの距離:H4=1
原点から六角形面までの距離:H6=√3(1−d/3)
以上により
表面積:S=6S4+8S6
=12(2−d)^2+4√3(−3+6d−2d^2)
=(12−8√3)d^2+(24√3−48)d+48−12√3
体積:V=6S4H4/3+8S6H6/3
=4(2−d)^2+4(−3+6d−2d^2)(1−d/3)
=8/3d^3−12d^2+12d+4
任意の切頂立方体は球に内接します.一方,球に外接(内接球が存在)するための条件は
√3(1−d/3)=1 → d=3−√3
となります.六角形面が正六角形となる切頂八面体ではd=3/2ですから,切頂八面体は球に外接しないことがわかります.
===================================
【3】区分多項式
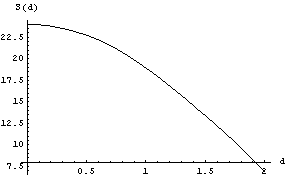
表面積関数Sも体積関数Vも区間0≦d≦2において単調減少関数であって,d=1で多項式を連続条件を満たすように接続した区分多項式となっています.実際にグラフを描いてみると滑らかに接続されているように見えます(阪本ひろむ氏のご好意による).
[1]Sのプロット図

[2]Vのプロット図
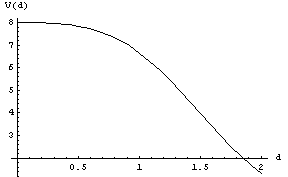
それでは導関数も連続となっているのでしょうか?
S=(4√3−12)d^2+24 → S(1)=4√3+12
S’=2(4√3−12)d → S’(1)=2(4√3−12)
S”=2(4√3−12) → S”(1)=2(4√3−12)
S=(12−8√3)d^2+(24√3−48)d+48−12√3 → S(1)=4√3+12
S’=2(12−8√3)d+24√3−48 → S’(1)=2(4√3−12)
S”=2(12−8√3) → S”(1)=2(12−8√3)
V=−4/3d^3+8 → V(1)=20/3
V’=−4d^2 → V’(1)=−4
V”=−8d → V”(1)=−8
V^(3)=−8 → V^(3)(1)=−8
V=8/3d^3−12d^2+12d+4 → V(1)=20/3
V’=8d^2−24d+12 → V’(1)=−4
V”=16d−24 → V”(1)=−8
V^(3)=16 → V^(3)(1)=16
この結果,関数Sは1次導関数まで連続となるような2次式,関数Vは2次導関数まで連続となるような3次式であることがわかりました.また,このことからS/V,S^3/V^2などもd=1で連続となることも理解されます.
S’V−SV’=0
3S’V−2SV’=0
についても同様です.
===================================
【4】S^3/V^2比の最小化
[1]S^3/V^2のプロット図
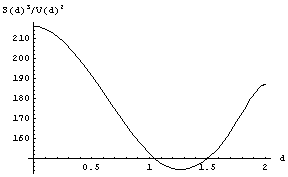
3S’V−2SV’=0
より,S^3/V^2が最小値をとるdを求めると
d=3−√3
となって,前述の内接球をもつための条件と一致しました.したがって,等周比の点からいうと,内接球をもつ「切頂14面体」が最も球に近いことになります.
なお,「切稜18面体」においてもS^3/V^2が最小値をとる条件と内接球をもつ条件とが一致しましたが,このことは正多面体の切頂多面体,切稜多面体についても一般的にいえることなのかもしれません.確かめたわけではありませんが・・・
[2]S/Vのプロット図

参考までにS/Vのプロット図を掲げておきますが,極小値を与えるdは0<d<1にあります.これを数値的に求めると
d=0.8960
となりました.
===================================
【5】まとめ
d=0・・・・・・・・・・・・・立方体
d=2−√2・・・・・・・・・・切頂立方体
d=0.8960・・・・・・・・S/V比が最小となる切頂14面体
d=1・・・・・・・・・・・・・立方八面体
d=3−√3・・・・・・・・・・球に外接(内接球が存在)し,かつ,S^3/V^2比が最小となる14面体
d=3/2・・・・・・・・・・・切頂八面体
d=2・・・・・・・・・・・・・正八面体
球に外接(内接球が存在)する切頂14面体は
d=3−√3
のみですが,それに対し,任意の切頂立方体は球に内接します.
===================================