今回のコラムではまず最初に,中川宏さんに頂いたメールを紹介したいと思います.
「きのうは先生の空間充填形のページを読ませていただいたのですが,よくわからないままでした.そして今日36°Cの猛暑の中での仕事を終えて冷房の効いた電車で帰途についたときに,じわっとわかってきました.
18面体と立方体とによる空間充填とは,18面体を隙間なく組んでいったときに18面体の表面の正方形で囲まれた立方体が隙間として残るということだったんですね.それで18面体だけで埋め尽くそうとすると立方体を小さくしていくことになるわけですが,そのためには18面体の面取りを深くして正方形を小さくしてやる必要がある.そしてついに正方形がなくなったとき出来ている形が菱形12面体と呼ばれているのですね.
つまり,先生が書かれている立方体単独による空間充填と菱形12面体単独による空間充填とを橋渡しするものとして,さまざまな面取り度合いの18面体と立方体との二種類の立体による空間充填を理解することができるということなんですね.こう言い換えてもいいわけですね.
立方体だけによる空間充填においてひとつおきの立方体を少しずつ収縮させてやる.そして残された立方体にはできた隙間を埋めるだけの肉付けをしてやる.その太ったほうが18面体.そしてついに収縮する立方体がきえてしまったときには空間は菱形12面体のみによって充填されている.ここまで理解できて初めて佐藤先生が私の作っている18面体に注目された理由がすこし理解できた気がいたします.」
まったくその通りです.これまでの話を整理しておきたいと思います.もとの立方体の1辺の長さを2,正方形面の1辺の長さをdとします(0≦d≦2).すると,
d=2・・・・・・・・・・・・・立方体
d=2(√2−1)・・・・・・・内接球をもつ18面体(d=2*0.4142)
d=2(4√3−3)/13・・・等稜18面体(d=2*0.3022)
d=0.4・・・・・・・・・・・外接球をもつ18面体
d=0・・・・・・・・・・・・・菱形十二面体
のように立方体の切稜によって菱形十二面体との中間段階にある18面体を作ることができます.
立方体と菱形十二面体は単独で空間充填可能ですが,その中間段階のさまざまな面取り度合いの切稜18面体は単独では空間充填できません.中川さんのご指摘の如く,切稜18面体は立方体単独と菱形十二面体単独による空間充填を橋渡しするものとして理解することができるというわけです.
===================================
【1】切稜18面体の計量
p角形面およびq稜頂点をもつ正多面体を,シュレーフリにしたがって
(p,q)
で表すことにしましょう.また,凸多面体の頂点,辺,面の数をそれぞれv,e,fとします.
多面体の切稜によって,辺は六角形面に,q本の辺の会する頂点はq角錐になります.一般に正多面体は(p,q),(v,e,f)で表されるわけですが,このことから,正多面体の切稜多面体(V,E,F)は
F=f+e
E=2e+qv
V=v+qv
で表されることがわかります.
立方体では(p,q)=(4,3),(v,e,f)=(8,12,6)ですから,その切稜多面体は
F=18,E=48,V=32
となります.もちろん切稜後もオイラーの多面体公式
V−E+F=v−e+f=2
は成り立ちます.
一般の多面体では
Σpi=p1+・・・+pf=2e,
Σqi=q1+・・・+qv=2e
正多面体では
pf=2e,qv=2e
となりますから,(V,E,F)を(v,e,f)だけで表すことにすれば
F=f+e
E=4e
V=v+2e
となります.
以下,切稜18面体に限って話を進めますが,計算を簡単にするためには,r=d/2(0≦r≦1)とおいて
r=1・・・・・・・・・・・・・立方体
r=√2−1・・・・・・・・・・内接球をもつ18面体(r=0.4142)
r=(4√3−3)/13・・・・等稜18面体(r=0.3022)
r=0.2・・・・・・・・・・・外接球をもつ18面体
r=0・・・・・・・・・・・・・菱形十二面体
とした方がわかりやすいかもしれません.
しかし,いずれにせよ切稜18面体の本質的なパラメータはただひとつであって,切稜18面体はパラメータdによってその形や表面積,体積が決定されます.
正方形面の頂点の座標:(d/2,d/2,1)
六角形面の頂点の座標:(d/4+1/2,d/4+1/2,d/4+1/2)
六角形面の中心の座標:(d/4+1/2,d/4+1/2,0)
ですから,
正方形面の面積:S4=d^2
六角形面の面積:S6=(3d/2+1)(1−d/2)/√2
また,
原点から正方形面の中心までの距離:H4=1
六角形面の中心までの距離:H6=(d/4+1/2)√2
以上により
表面積:S=6S4+12S6
=(6−9/√2)d^2+6√2d+6√2
=(24−36/√2)r^2+12√2r+6√2
体積:V=2S4H4+4S6H6
=−3/4d^3+3/2d^2+3d+2
=−6r^3+6r^2+6r+2
が得られます(0≦d≦2,0≦r≦1).
===================================
【2】S/V比の最小化
ところで,
(問)ビールの泡のひとつひとつが同じ体積だと仮定して,表面張力で泡と泡の境界の総面積が最小になるとき,泡はどんな形か?
すなわち,空間を体積が等しい凸多面体で,平均表面積ができるだけ小さくなるように分割せよという問題を考えることができます.
この問題はかなり長い間,菱形12面体による空間分割が解だと考えられていたのですが,これに対して,体積1のときの表面積を求めると,菱形12面体型分割では
3√108√2=5.345・・・
切頂8面体型分割では
3/43√4(1+√12)=5.314・・・
と後者の方が約0.5%少なくなることが,1887年,英国の物理学者ケルビン卿によって発見されています.
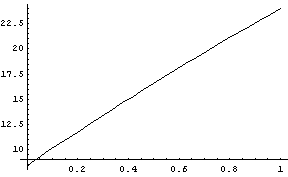
この節では問題の意図を少し変えて,最小の表面積で最大の体積を有する切稜18面体がどのような形になるかを考えてみたいのですが,畏友・阪本ひろむ氏に以下のグラフを描いてもらいました.
(1)S

(2)V
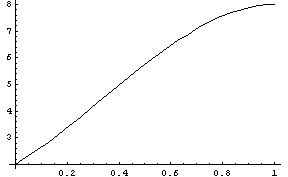
(3)S/V
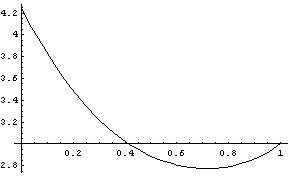
S,Vが0≦r≦1の範囲で単調増加になることは容易にわかりますが,S/Vはそうはならず,グラフよりr=0.7付近で最小値をとります.そして
S’V−SV’=0
より,S/Vが最小値をとるrを求めると
r=0.7159
となりました.
===================================
【3】S^3/V^2比の最小化
[1]平面凸集合に関して,周の長さLが一定で面積Aが最大の図形(面積が一定で周の最小な図形)は円であるという事実は古代ギリシアの時代からよく知られています.そのことはL^2≧4πAという不等式で表現されます.等号は円のときだけ成立します.
同様に,3次元凸集合に対し,表面積をS,体積をVとするとS^3≧36πV^2が成り立ちます.等号成立は球のときだけで,すべての立体中で球が表面積に対して最大の体積をもっています.
等周不等式は,平均曲率一定曲面と密接な関わりをもっています.凸体Vを囲む曲面Sにおいて,平均曲率は,
H=1/2(1/R1+1/R2)
で定義されます.ここで,平均曲率の積分を
M=∫Hds
で表すと,ミンコフスキーの不等式
S^2−3VM≧0
M^2−4πS≧0
これから直ちに
S^3≧36πV^2
が導かれます.
ところで,
(1)シャボン玉はなぜ丸くなるのでしょうか?
(2)クマはなぜ丸くなって冬眠するのでしょうか?
S^3≧36πV^2に関係していることは直感的に発想できるでしょう.クマやリスなど動物達は(この定理を知っているから)丸くなって冬眠しますが,(この定理を知らない)酔っぱらいのオヤジは往来に大の字になって寝ていて凍死するはめになるというわけです.
===================================
[2]さて,立体図形のS^3/V^2は平面図形のL^2/Aの相当していて,「等周比」あるいは「等周定数」と呼ばれます.ここではS/Vではなく,S^3/V^2が最小値をとるrを求めたいと思います.
(4)S^3/V^2
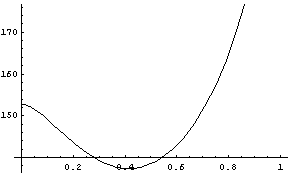
3S’V−2SV’=0
より,S^3/V^2が最小値をとるrを求めると
r=√2−1
となって,切稜18面体が内接球をもつ条件と一致しました.したがって,等周比の点からいうと,内接球をもつ切稜18面体が最も球に近いことになります.
===================================
球に内接する多面体が存在すること自体が稀なのですが,与えられた球に対して球面上に勝手に点をうって接平面を作っていけば,内接球をもつ立体を作ることができます.(一方,外接球にすべく,勝手に取った点をつないで線は引けても,面を構成するには相手を選んで線を引かねばならないし逐次的にいくのも大変です.)
球面上にn個の点を配置した場合,n個の頂点(またはn個の面)をもつ凸多面体の内接球半径rおよび外接球半径Rの間には,球殻不等式
R/r≧√3tanωn
ωn=n/(n−2)・π/6 n≧3
が成立します.n=4のとき,ωn=π/3.したがって,
R/r≧3 (4面体不等式)
が得られます.
この3次元版の球殻不等式から「同じ大きさの球に内接する正12面体と正20面体とでは,正12面体の方が体積Vも表面積Sも大きい.」が導かれます.そんなばかなと思われるかもしれませんが,直感に反して,正12面体は球の66.5%,正20面体は球の60.6%を占めるのです.したがって,正多面体を球に内接させたとき最も球に近い正多面体は正12面体です.(一方,外接させれば体積も表面積も正20面体の方が球に近くなります.)
また,多面体の等周問題は,単位球に外接する多面体の場合,
V=S/3
となることから,
S^3/V^2=9S=27V
が成り立ちます.したがって,与えられた面数nをもつ多面体に関する等周問題は,最小の体積または最小の表面積をもち,球に外接するn面体を定めるという問題に帰着されます.
等周比の点からいえば,5種の正多面体では正4面体が最も球に遠く,正20面体が最も球に近いことになります.それでは,f個の面をもつ多面体の中で等周比の最小値を与えるものはなんでしょうか?
答えはf=4,6,12ではプラトンの正多面体,すなわち,正四面体,立方体,正十二面体が最小値をとります.しかし,f=8で等周比の最小値をあたえるものは正八面体ではありません(アルキメデスの反プリズム).f=20は未解決のまま残っています.
===================================
[3]この節では,
L^2≧4πS (2次元等周不等式)
S^3≧36πV^2 (3次元等周不等式)
をどんな次元にも適用できるように公式化してみましょう.
半径rのn次元超球の体積はVnr^n,表面積はnVnr^(n-1)となりますから,等周比を無次元化するために,
n次元等周比=表面積^n/体積^(n-1)
と定義すると,
n次元等周比≧n^nVn=n^nπ^(n/2)/Γ(n/2+1)(=Cn)
を得ることができます.等号は超球のときに限ります.
この証明はVn=π^(n/2)/Γ(n/2+1)がn次元単位球の体積であることが理解できれば簡単です.n次元等周比(Cn)において,とくに,n=2のときとn=3のときについては,
C2=4π
C3=36π
すなわち,
L^2≧4πS
S^3≧36πV^2
になることがわかります.
以下,
C4=2^7π^2
C5=8/3*5^4π^2
C6=6^5π^3
・・・・・・・
となりますが,等周比が有理数(整数)×πの形となるのは,2次元・3次元だけのようです.
===================================
【4】まとめ
r=1・・・・・・・・・・・・・立方体
r=0.7159・・・・・・・・S/V比が最小となる18面体
r=√2−1・・・・・・・・・・内接球をもつ18面体(r=0.4142)かつ
S^3/V^2比が最小となる18面体
r=(4√3−3)/13・・・・等稜18面体(r=0.3022)
r=0.2・・・・・・・・・・・外接球をもつ18面体
r=0・・・・・・・・・・・・・菱形十二面体
===================================
[参]フェイェシュ・トート「配置の問題−平面・球面・空間における−」みすず書房
===================================