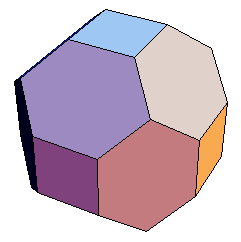
正多面体の頂点を削り落とすと,その中間段階でいろいろな準正多面体が得られます.たとえば,立方体の頂点を次第に削りとると,立方体(cube)→切頂立方体(truncated cube)→立方八面体(cuboctahedron)→切頂八面体(truncated octahedron)→正八面体(octahedron)と移行します.
最終的には立方体の双対多面体である正八面体が得られますが,中間形の切頂立方体,立方八面体,切頂八面体はいずれも準正多面体です.反対に,正八面体の頂点を削っていくと,正八面体→切頂八面体→立方八面体→切頂立方体→立方体ができあがります.
切頂八面体は名前のとおり正八面体の各辺を三等分して頂点を切り取った後に残る多面体です.実は,16種類の準正多面体のなかで空間充填が可能なのは切頂八面体−−正6角形8枚と正方形6枚の2種類で作る14面体−−しかありません.切頂八面体は体心立方格子のボロノイ多面体です.
また,立方体の各辺の中点を結んで頂点を切り落とすと,6枚の正方形と8枚の正三角形の合計14面からなる準正多面体ができます.正八面体についても12本の辺の中点を結んでその頂点を切り落とすと全く同じ多面体ができます.このように立方八面体は立方体と正八面体の両方から中点を結ぶという同じプロセスでできあがる準正多面体です.
日本では古くから灯篭などの照明器具などに立方八面体の形をした装飾品が使われ親しまれていますから,この立体をご存じの方も多いと思います.立方八面体は単独では空間充填形ではありませんが,正八面体と組み合わせると空間充填が可能です.
また,サッカーのボールは正五角形12個と正六角形20個を張り合わせてできていますが,この準正多面体は正20面体(頂点が12個,正三角形の面が20個ある)の各頂点からのびている5本の辺をそれぞれ1/3の長さの所で切り取り,五角錐をはずした姿であり,切頂二十面体(truncated icosahedron)とも呼ばれます.
このように正多面体の頂点を削り落とすことによって新たな多面体が作られるのですが,それでは各辺を削り落とす(面取りする)ことによってどのような多面体が得られるのでしょうか? このような発想はこれまで盲点となっていて,あまり取り上げられることがなかったように思われます.
先日のことですが,山口県防府市の中川宏さんから頂いたメールでこのことにはっとさせられました.今回のコラムでは「切稜立方体」について,中川さんと小生,それに小川泰先生との間で行われたやりとりについて紹介したいと思います.
===================================
(1)中川→佐藤
突然の問い合わせメールで失礼いたします.「多面体 照明」で検索したところ貴サイトを発見し,多面体研究に明るい方とお見受けいたしました.立方八面体が日本古来からの灯篭に使用されているということをお聞きして大変興味を持ちました.
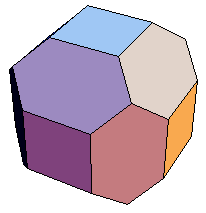
わたしは山口県山口市の中井産業株式会社という木材加工会社に勤めていまして,趣味で立方体のすべての稜を45度等距離で切り落とした18面体を組み立てて照明器具などを作っております.
お忙しいことと思いますが,なにかの機会にわたしのページをごらん頂き,日本古来からの灯篭についてお教えいただければ幸いです.
中井産業株式会社
積み木インテリアギャラリー<http://ww6.enjoy.ne.jp/~hiro-4/>
中川宏<hiro-4@do6.enjoy.ne.jp>
===================================
(2)佐藤→中川
拝見いたしました.頂点を中心に削り落とした形はよく見かけるのですが,中川さんのように辺を削り落とすという発想の形は初めてみたように思います.興味深い形でありますが,浅学のためなんと読んだらいいのかあるいはなんと呼ばれている形なのかわかりません.小川泰先生にご教示してもらいたいと存じます.
===================================
(3)佐藤→小川
不躾なメールお許しください.小生,趣味で数学や形を取り扱っている者で,だいぶ以前ですが先生からメールを頂戴したことがございます.
先ほど木工会社勤務の方より受けた質問なのですが,浅学のため回答できなかったものがあります.その方のHP:http://ww6.enjoy.ne.jp/~hiro-4/を拝見したところ,面白い形の18面体による造形が掲載されています.HPではくるくる回転する立体が出てきますが,それは6枚の正方形と12枚の六角形(正六角形ではない)からできる立体です.
その形とは立方体の辺をカンナで削り落としたものになっています.中川氏は木工会社勤務ということなのですが,立方体の辺の部分を面取りすると自然にこの形が現れるようです.
立方体の頂点を削り落とすと,切頂八面体や立方八面体ができることはよく知られていますが,このような形は見たことがなく,しかもこの立体をもとに色々な造形(たとえば切頂八面体型に組み上げることができる)が可能ということでした.
正多面体→準正多面体の過程を考えると「頂点を削る」ことだけに関心を奪われ「辺を削る」ことをすっかり忘れてしまっていたのですが,氏よりのメールでこのことに気がつきました.木工会社勤務ならではの発想と思い知った次第であります.
ところでこの立体はなんと命名されているのですか? 正六角形ではないのでおそらく名前がついていないのではと思われるのですが,工芸品にもあまり使われることのない形です.なんと呼ぶべきかあるいはなんと呼ばれている立体なのかわかりません.また何か工芸装飾品への応用例はないものでしょうか? ご存知でしたらご教示願います.
===================================
(4)小川→佐藤
HPではまだ確認しておりませんが,この情報で見当がつきました.立方体の12稜すべてを両側の2面を同等に扱って,ある深さまでカンナをかけます.3稜が集まる立方体の頂点の所ではカンナ掛けで現れた3面が出逢って結局カンナ掛けで現れた12面は6角形に.理想的にいけば,六角形の内角は対称軸上の2角の大きさがArccos(-1/3),その他の角度はArccos(-1/√3)別の表現では,立方体の各面に正4角錘台を貼り付けたともいえましょう.
Mathematicaで書いてみました.添付します.正方形頂点の座標は(1,1,3)型で,3枚の6角形が集まる頂点座標は(2,2,2)型です.

お書きになったことを頼りに推測しただけで,私にとっても初見です.準正多面体には該当しないので,名前は特に付いていないように思います.以前ボロノイ分割の整理で分類したときの考えでは,高対称の[060Y]とでも名付けておきます(Yは12を表すつもり).3角4角の順に面数を列挙し,0の無限列は省略.「木工」に関わる何かの表現を入れた方がいいと思いますが,今のところノーアイディアです.
===================================
(5)中川→佐藤
くわしくみていただいて光栄です.じつはわたしもこの18面体の名前を知りたくて数名の多面体研究家のかたがたに相談したのですが,どうやらこれまでに名前をつけた人はいないようでした.ご指摘のとおり,多面体の世界では頂点を切り落として準正多面体を作るという方法が一般的なようで,当初はこの18面体もその類かと思っていたのですが,「ちゃーりー田中」<http://chahix.ddo.jp/~chahi/cha_polyhedron_home/tamenroom/7.html>さんとのやりとりのなかで,切っているのは頂点ではなく稜であることにようやく気がついた次第です.おそらくは数学的にはこの18面体の六角形は正六角形ではないので,関心をもたれることはなかったのだろうと思っています.
わたしはもっぱら木工のほうから出発していまして,木工の世界では面取りというごくありふれた技法にすぎません.ただおもいきって断面が正8角形になるまで深くしただけなのです.ですから名前をつけるとしても「面取りした立方体」とかすこし数学らしく「切稜立方体」くらいしかおもいつきません.ほんのすこしでも佐藤さんの研究のお役に立てばいいのですが.
かねがね手毬の模様に多面体が使われてきたことを教えていただき,なんとなく自分の作っているものに「和」を感じることがあったのですが,日本古来の灯篭に立方八面体が使われてきたという佐藤さんのご指摘を目にして,やっぱりそうだったんだと,ルーツを教えていただいたように感じた次第です.ぜひ写真でも,実物のある場所でもおしえていただければありがたいです.
大変お忙しいなか,日本物理界の大先生にご検討いただいてまことに恐縮しております.小川先生にはわずかな情報からつくりかたまでご理解いただいてたいへんうれしくおもっています.
わたしには中学程度の数学の知識しかありませんが,送っていただいた小川先生の作図をみせていただいて量的には少し違うように感じましたので,お粗末な図を添付いたします.
===================================
(6)佐藤→中川
私は小川先生とは面識ありませんが,メールではこれまで何回か情報交換したことがありました.確かに小川先生の図は中川さんのものより六角形部分が大きく感じられます.このメールも転送して再検討してもらうことにしたいと存じます.
===================================
(7)佐藤→小川
木工会社勤務の中川さん<hiro-4@do6.enjoy.ne.jp>より次のようなメールが届きました.先生の描かれた切稜立方体の六角形部分が中川氏のものより大きすぎるというのです.切稜立方体には何種類かあり,いろいろなタイプの切稜立方体が作れるのかもしれません・・・.
===================================
(8)小川→佐藤
中川さんのメール転送等有難うございました.お返事が遅れましたが,前回のが菱形12面体と立方体との共通領域として,もっと一般化できることに気づき,その中でも特別のものとして射影が正8面体になる場合があると考えておりました.
中川さんのはその場合に相当すると推測します.(まだ詳しく調べておりません).それらの図を作るのに単純ミスがあって手間取っておりました.4枚ほど添付致します.
1 菱形12面体 頂点は(2,0,0)型と(1,1,1)型
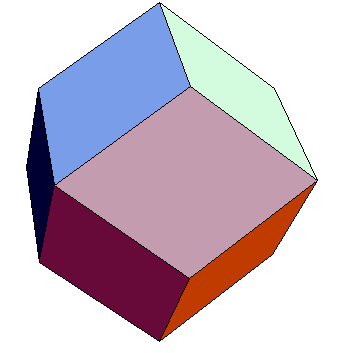
2 射影輪郭が正8面体になるように4価の6頂点を切頭
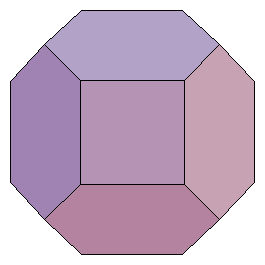
3 6角面だけで表示
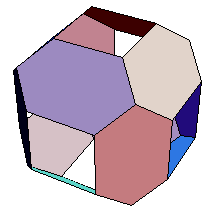
4 中川さんのはこの場合(今図を見ると間違いありません)
[補]菱形十二面体は対角線の長さの比が1:√2の合同な菱形を12枚張り合わせたものです.菱形十二面体はざくろ石の結晶としても自然界に産出し,その投影図は正面,平面,側面がすべて正方形になっているという奇妙な投影図形を示します.
菱形十二面体は,面が正多角形ではないので準正多面体ではありませんが,立方八面体の各面の中心をつないで余分なところを切り落とすと現れる多面体,すなわち,準正多面体の双対多面体でもありますから一種の準正多面体群として考えることができます.このように,プラトン立体の双対は正多面体ですが,アルキメデス立体の双対は準正多面体とは異なる一群の立体となります.
正多面体による空間充填を考えると,立方体は明らかに空間を埋めつくすのですが,立方体を除く正多面体はどれも空間を充填しません.5種類ある正多面体(プラトン立体)の中では立方体だけ,16種類ある準正多面体(アルキメデス立体:2種類以上の正多角形から構成されている立体)の中では切頂八面体だけが空間を単独で埋めつくすことができます.
また,それ以外の単独空間充填形となる多面体としては,菱形十二面体(rhombic dodecahedoron )があげられます.菱形十二面体は,面が正多角形ではないので準正多面体ではありませんが,面心立方格子のボロノイ多面体になっています.
===================================
(9)佐藤→小川
ありがとうございました.このメールも中川さんに転送しておきました.確かに4は中川さんのものに間違いないようです.
今後「切稜多面体」に関していくつかの研究がなされることが予想されるのですが,先生が切稜多面体を立方体のみならず正四面体などにも試された解説記事が読める日を待っております.
===================================
(10)中川→佐藤
小川先生のご研究の進展をたのしみにいたしております.わたしが作っている18面体は断面が正8角形になる,つまり18面体のすべての面が球に外接するという特性がありますが,小川先生が最初に理想的とお考えになった形はすべての稜が同寸という特性があるようにお見受けいたしました.
さらに球に内接する18面体というのも求めることが出来そうですね.それらは組み立てるとどんな形になるのでしょうか? 興味深いところです.
===================================
その後,中川さんより切稜立方体で組み立てた切頂8面体型のランプが贈られてきました.実物はまるで分子模型のようでありますが,木工会社勤務の本職の方が作られたものだけに大変恐縮してしまいました.
(11)佐藤→小川
中川さんから贈られた18面体を切頂八面体状に組み上げましたものを実際に手にすると,18面体と立方体を組み合わせた2種類の立体による空間充填が可能であることがわかります.
したがって,先生が示されましたように,菱形十二面体には1つの頂点に3面が会するところと4面が会するところがある→4面が会する頂点を切頂して屋根型に切り取る→屋根(立方体を6分割した扁平な四角錐)が6個で立方体になる.こうして中川さんのオブジェが菱形十二面体による空間充填の変形になっている様子を容易に窺い知ることができるようになります.
また,中川さんは最初の図(辺の長さが同寸)にも大変興味をもたれているようで,小川先生の「勘違い」から派生した最初の図も大変有益なものと考えられます.これも是非HPで紹介したいと考えておりますが,如何でしょうか?
===================================
[補]それほど単純でない単独空間充填多面体の例としては,切頂4面体の正三角形部分に正4面体を4分割した扁平な4面体をくっつけたものが知られていますし,また,対称性をもたない凸の空間充填多面体としては,38面体の例も知られているようです.
もし2種類以上を使ってよければ,正四面体と正八面体の二面角が互いに補角ですから,両者を組み合わせて空間充填が可能になります.一種類の合同な正多面体による空間充填では立方体だけが空間充填形なのですが,正多面体同士の組合せでは,正四面体と正八面体を組み合わせたものだけが空間を充填します.
一方,2種類以上の多面体による空間充填については,すでに述べた切頂4面体と正4面体(1:1),切頂立方体と正8面体(1:1),切頂8面体と切頂立方8面体と立方体(1:1:3)の組合せなど,非常に多くの例があります.
===================================