日本人の名前を冠した折り紙定理

［定理］折り紙のひとつの角が辺の中点に来るように折る．このときできる３つの直角三角形はいずれもエジプト三角形（３辺の長さ比が３：４：５の直角三角形）である（芳賀和夫の定理）．

には，辺の中点に加えて，辺の３等分点が現れた．

　この定理とコラム「数楽と音学における３：４：５定理」で証明した「平行四辺形における３：４：５定理」の間には何らかの関連性があるのだろうか？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】平行四辺形における３：４：５定理

　平行四辺形の頂点Ａ，Ｂ，Ｃ，Ｄをそれぞれ辺ＢＣ，ＣＤ，ＤＡ，ＡＢの中点と結んで，中央に小さい平行四辺形を作る．この小さい平行四辺形の面積は，もとの平行四辺形の面積の１／５に等しい．次に，平行四辺形の頂点Ａ，Ｂ，Ｃ，Ｄをそれぞれ辺ＣＤ，ＤＡ，ＡＢ，ＢＣの中点と結んでも中央に小さい平行四辺形が得られる．この小さい平行四辺形が重なった部分は点対称な８角形で，その面積はもとの平行四辺形の面積の１／６に等しい．

　このとき，重なっている小さい平行四辺形は互いの辺を３等分するのではなく，辺を分割する比は４：５：３になっている．

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

　平行四辺形の頂点と２等分点を使ったダイヤグラムでは，平行四辺形の重なりにおいて，４：５：３の比があらわれた．では，３等分点を使ったダイヤグラムではどうだろうか？

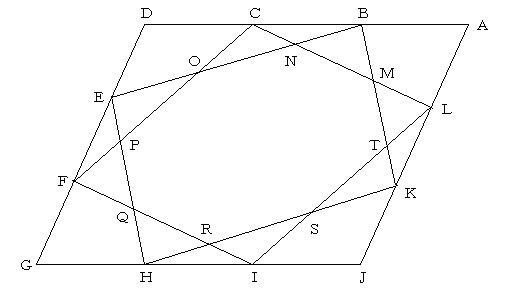
　求めるのは，ＥＯ：ＯＮ：ＮＢであるが，４：５：３になっていることが証明される．平行四辺形の辺を３等分すると「３：４：５定理」が得られるのであるが，こんなところにも直角三角形に関係する３：４：５があるのかと驚かされた．偶然の一致として片づけてしまってもいいのだろうか？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝