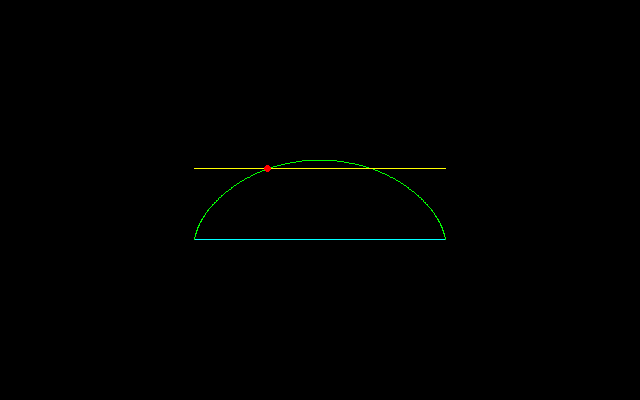
【１】サイクロイド弧長のｎ等分

　　２ｒ（−２ｃｏｓ（ｔ／２）＋２）＝８ｒ／ｎ

　　−２ｃｏｓ（ｔ／２）＋２＝４／ｎ

　　ｃｏｓ（ｔ／２）＝１−２／ｎ

　　ｙ＝ｒ（１−ｃｏｓｔ）＝ｒ（２−２ｃｏｓ^2（ｔ／２））＝２ｒ（１−（１−２／ｎ）^2）

［１］３等分する場合，

　　ｙ＝２ｒ・８／９，ｔ＝２ａｒｃｃｏｓ１／３

［２］４等分する場合，

　　ｙ＝２ｒ・３／４，ｔ＝２ａｒｃｃｏｓ１／２＝２π／３

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

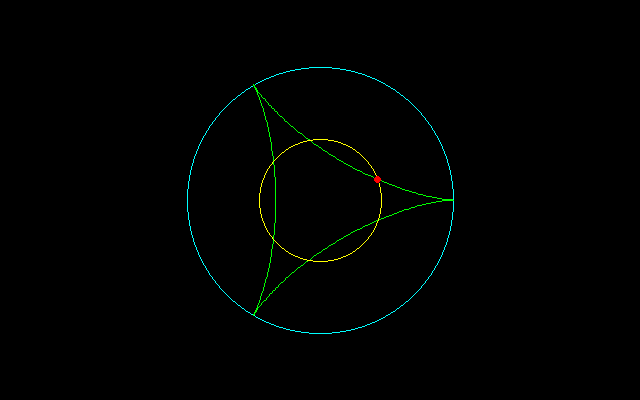
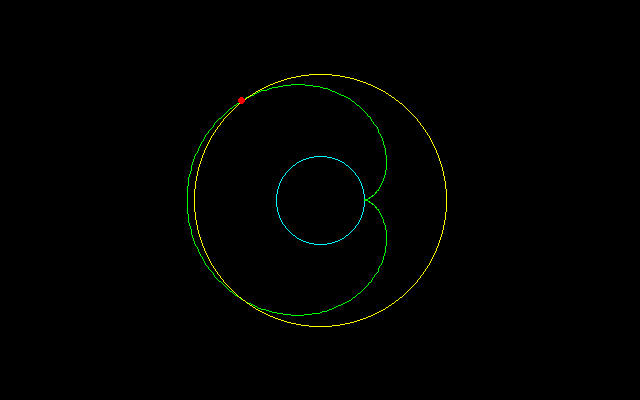
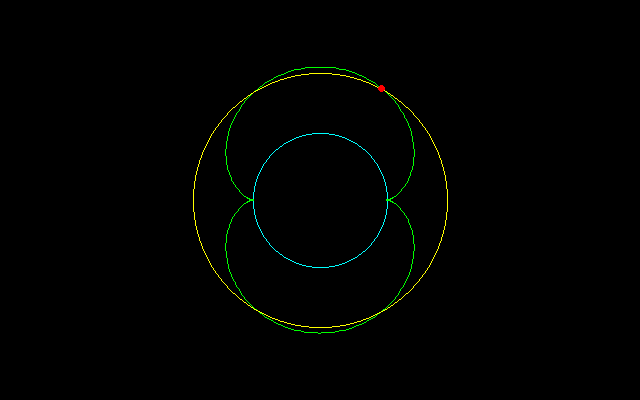
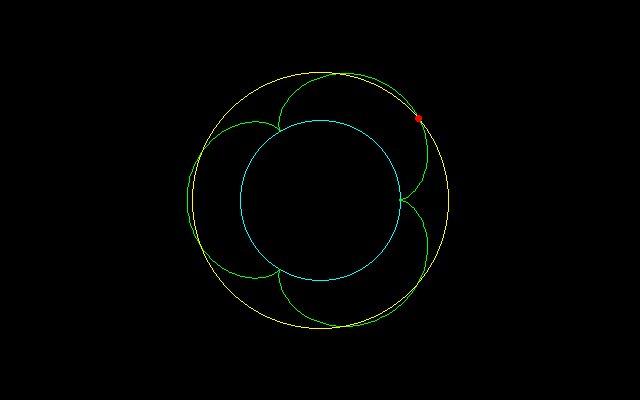
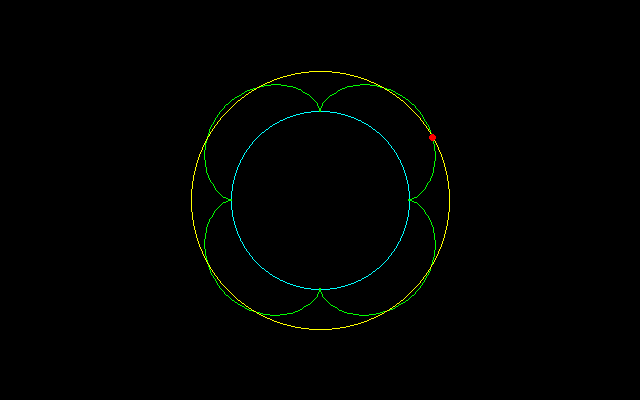
【２】内サイクロイド弧長のｍ等分

　　４（ｎ−１）／ｎ（−ｃｏｓ（ｎｔ／２）＋１）＝８（ｎ−１）／ｍｎ

　　−ｃｏｓ（ｎｔ／２）＋１＝２／ｍ

　　ｃｏｓ（ｎｔ／２）＝１−２／ｍ

　　ｒ^2＝ｘ^2＋ｙ^2＝（ｎ−１）^2＋１＋２（ｎ−１）ｃｏｓｎｔ＝（ｎ−１）^2＋１＋２（ｎ−１）｛２ｃｏｓ^2（ｎｔ／２）−１｝＝（ｎ−１）^2＋１＋２（ｎ−１）（１−８／ｍ−８／ｍ^2）

［１］３等分する場合，

　　ｒ^2＝（ｎ−１）^2＋１−１４（ｎ−１）／９

　　ｔ＝２／ｎ・ａｒｃｃｏｓ１／３

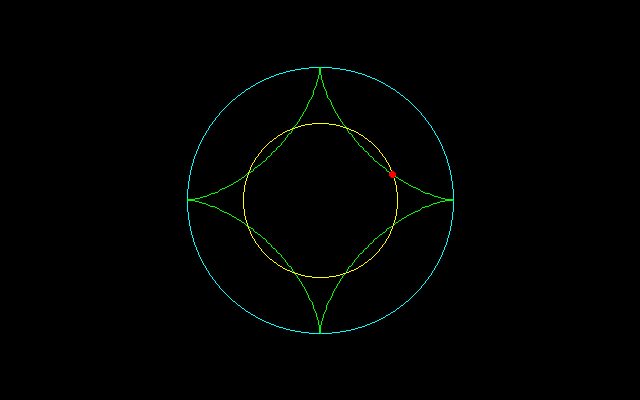
［２］４等分する場合，

　　ｒ^2＝（ｎ−１）^2＋１−（ｎ−１）

　　ｔ＝２／ｎ・ａｒｃｃｏｓ１／２＝２π／３ｎ

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

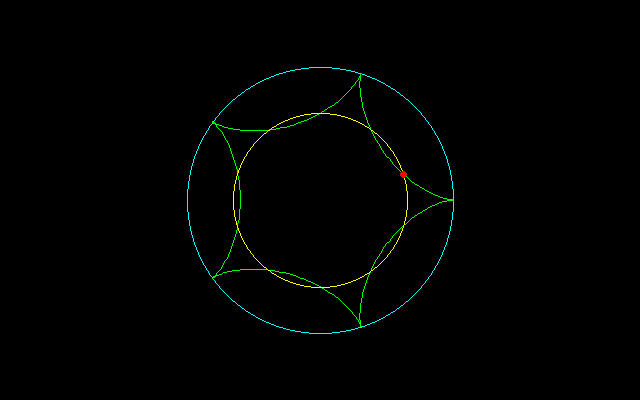
【３】外サイクロイド弧長のｍ等分

　　４（ｎ＋１）／ｎ（−ｃｏｓ（ｎｔ／２）＋１）＝８（ｎ＋１）／ｍｎ

　　−ｃｏｓ（ｎｔ／２）＋１＝２／ｍ

　　ｃｏｓ（ｎｔ／２）＝１−２／ｍ

　　ｒ^2＝ｘ^2＋ｙ^2＝（ｎ＋１）^2＋１−２（ｎ＋１）ｃｏｓｎｔ＝（ｎ＋１）^2＋１−２（ｎ＋１）｛２ｃｏｓ^2（ｎｔ／２）−１｝＝（ｎ＋１）^2＋１−２（ｎ＋１）（１−８／ｍ−８／ｍ^2）

［１］３等分する場合，

　　ｒ^2＝（ｎ＋１）^2＋１＋１４（ｎ＋１）／９

　　ｔ＝２／ｎ・ａｒｃｃｏｓ１／３

［２］４等分する場合，

　　ｒ^2＝（ｎ＋１）^2＋１＋（ｎ＋１）

　　ｔ＝２／ｎ・ａｒｃｃｏｓ１／２＝２π／３ｎ

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝