周長が

　　∫(0,x)1/(1-x^n)^(1/2)dx　　　(n=1~6)

で与えられる曲線については

［１］任意等分可能・・・・・・カージオイド

［２］２^mΠｐi 等分可能・・・円，レムニスケート

［３］２^m等分可能・・・・・・ｒ^3/2＝ｃｏｓ（３θ／２），ｒ^3＝ｃｏｓ（３θ）

［４］２等分すら不可能・・・・ｒ^5/2＝ｃｏｓ（５θ／２）

と分類できるようである．

　２等分可能な曲線は４等分，８等分も可能であったが，［３］［４］の間に

［ｘ］２等分しかできない曲線

があってよいはずである．

　今回のコラムでは（その６６）（その６９）で述べたサイクロイドの２等分点を図示してみたい．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】サイクロイドの場合

　サイクロイド：ｘ＝ｒ（θ−ｓｉｎθ），ｙ＝ｒ（１−ｃｏｓθ）

　　ｃｏｓ（ｔ／２）＝１−２／ｎ

　　ｎ＝２のとき，ｔ／２＝π／２→ｔ＝π（ｙ＝ｒ）

　　ｎ＝４のとき，ｔ／２＝π／３→ｔ＝２π／３（ｙ＝３ｒ／２）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

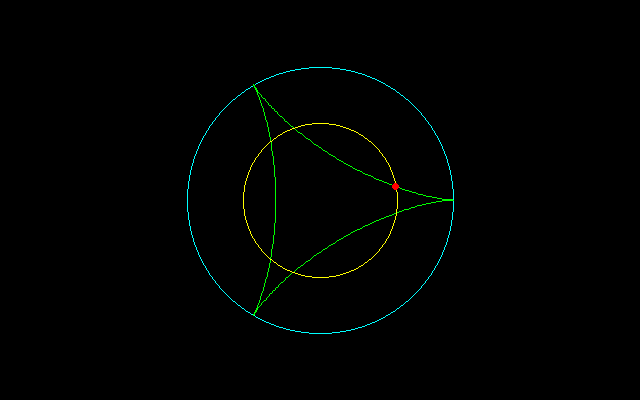
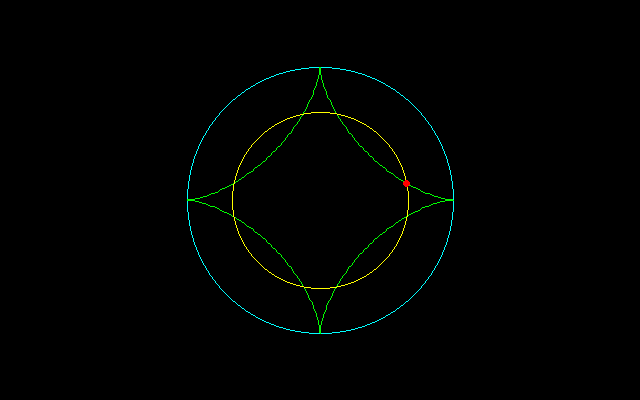
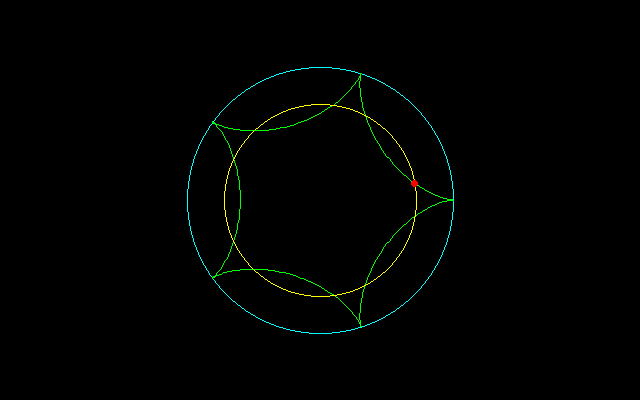
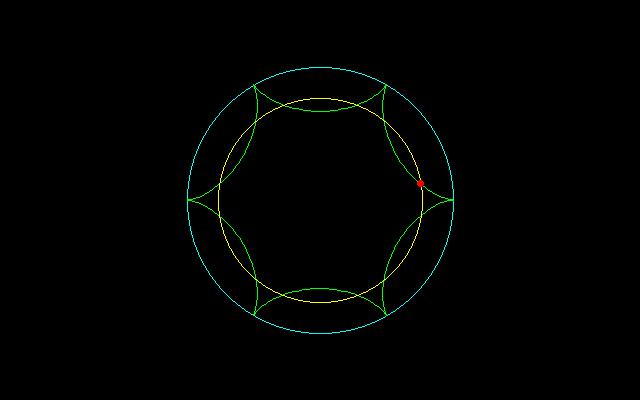
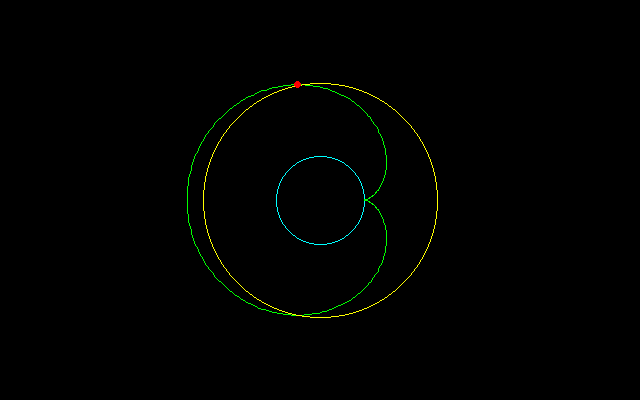
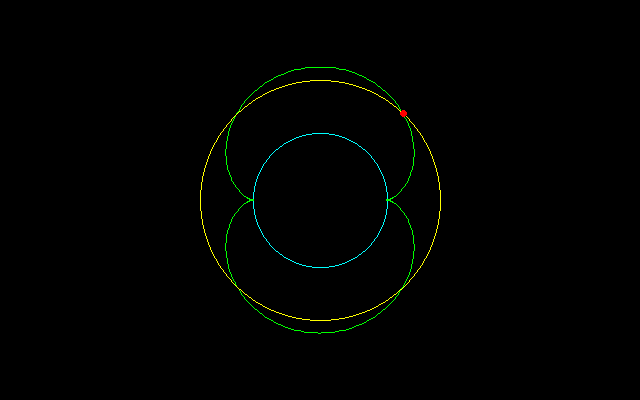
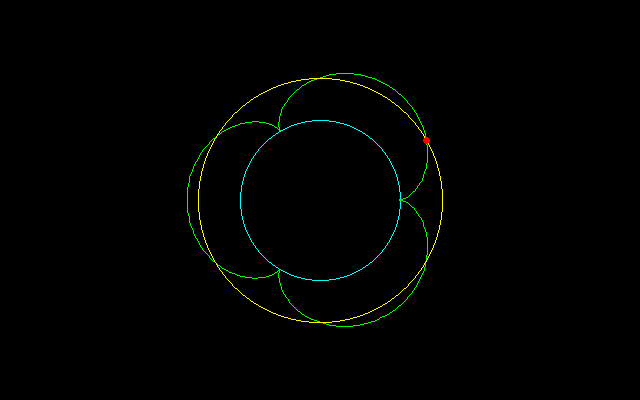
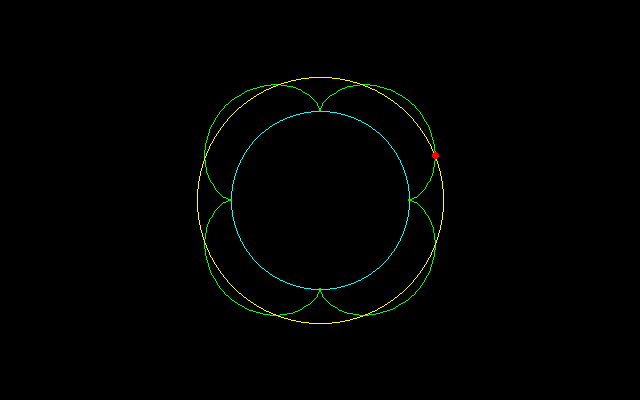
【２】内サイクロイドの場合

　　大円の半径：ｎ，小円の半径：１　　　（０＜ｔ＜２π／ｎ）

とする内サイクロイド

　　ｘ＝（ｎ−１）ｃｏｓｔ＋ｃｏｓ（ｎ−１）ｔ

　　ｙ＝（ｎ−１）ｓｉｎｔ−ｓｉｎ（ｎ−１）ｔ

について調べてみたい．

　　ｃｏｓ（ｎｔ／２）＝１−２／ｍ

　　ｍ＝２のとき，ｎｔ／２＝π／２→ｔ＝π／ｎ

　　ｍ＝４のとき，ｎｔ／２＝π／３→ｔ＝２π／３ｎ

　　ｒ^2＝ｘ^2＋ｙ^2＝（ｎ−１）^2＋１＋２（ｎ−１）ｃｏｓｎｔ

＝（ｎ−１）^2＋１−２（ｎ−１）＝（ｎ−２）^2　　　ｔ＝π／ｎのとき

＝（ｎ−１）^2＋１−（ｎ−１）　　　　ｔ＝２π／３ｎのとき

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【３】外サイクロイドの場合

　　大円の半径：ｎ，小円の半径：１　　　（０＜ｔ＜２π／ｎ）

とする外サイクロイド

　　ｘ＝（ｎ＋１）ｃｏｓｔ−ｃｏｓ（ｎ＋１）ｔ

　　ｙ＝（ｎ＋１）ｓｉｎｔ−ｓｉｎ（ｎ＋１）ｔ

について調べてみたい．

　　ｃｏｓ（ｎｔ／２）＝１−２／ｍ

　　ｍ＝２のとき，ｎｔ／２＝π／２→ｔ＝π／ｎ

　　ｍ＝４のとき，ｎｔ／２＝π／３→ｔ＝２π／３ｎ

　　ｒ^2＝ｘ^2＋ｙ^2＝（ｎ＋１）^2＋１−２（ｎ＋１）ｃｏｓｎｔ

＝（ｎ＋１）^2＋１＋２（ｎ＋１）＝（ｎ＋２）^2　　　ｔ＝π／ｎのとき

＝（ｎ＋１）^2＋１＋（ｎ＋１）　　　　ｔ＝２π／３ｎのとき

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝