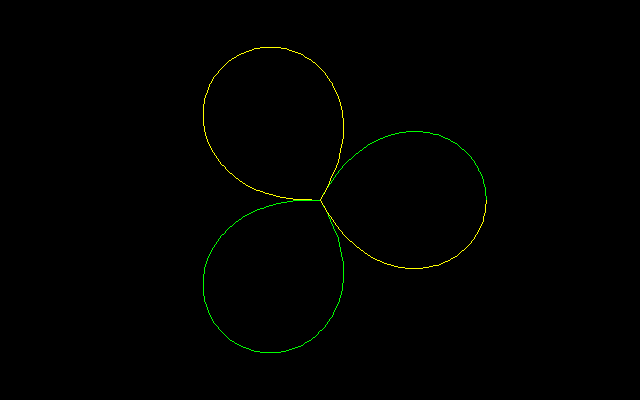
これで残る問題は（３，２）＝△の作図可能性ということになったが，ワイエルシュトラスのペー関数はもはや使えない．しかしながら，

　　Ｉ＝∫ｄｘ／（１−ｘ^3）^1/2

は第１種楕円積分となることが示される．

　ところで，第１種楕円積分の標準形

F(k,x)=∫(0,x)1/{(1-x^2)(1-k^2x^2)}^(1/2)f(x)dx

については加法公式

　　ｚ＝｛ｘ（１＋ｍｙ^2＋ｎｙ^4）^1/2＋ｙ（１＋ｍｘ^2＋ｎｘ^4）^1/2｝／（１−ｎｘ^2ｙ^2）

　　ｍ＝−（１＋ｋ^2），ｎ＝ｋ^2

が使える．

　そこで，積分Ｉに対応する半三つ葉型の中間曲線（１２次曲線）

　　ｒ^(3/2)＝ｃｏｓ（３／２θ）

　　（２（ｘ^2＋ｙ^2）^3−４ｘ^3＋３ｘ（ｘ^2＋ｙ^2））^2＝（ｘ^2＋ｙ^2）^3

のｋ等分点を求めてみようというのが今回のコラムの狙いである．

　中間曲線のグラフは半三つ葉型（緑）であるが，以下の図には実の部分（緑）に加えて虚の部分（黄）も描いてある．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

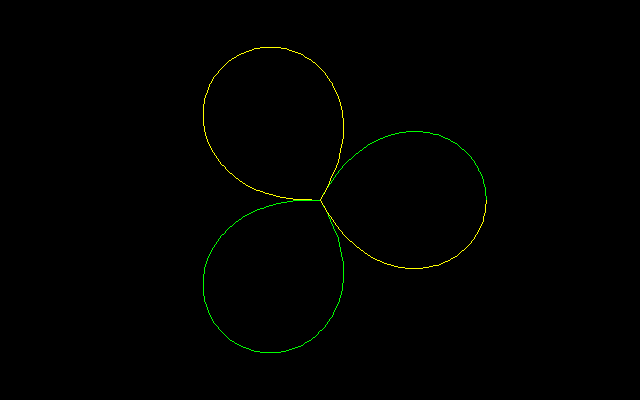
【１】第１種楕円積分の標準形への還元

　積分

　　Ｉ＝∫(c,1)ｄｘ／（１−ｘ^3）^1/2

を考える．変換

　　ｙ＝（λｘ＋μ）／（νｘ＋ρ），ｘ＝（−ρｙ＋μ）／（νｙ−λ）

を適当に選ぶことにより，常に

　　ｄｙ／（１＋ｍｙ^2＋ｎｙ^4）^1/2

の形に還元できる．

　　λ＝−１，μ＝１−√３，ν＝１，ρ＝−１＋√３

　ｘ＝ｃに対するｙの値を

　　ｙ1＝（ｃ−１＋√３）／（−ｃ＋１＋√３）

とおくと

　　Ｉ＝１／4√３∫(y1,1)２ｄｙ／（（１−ｙ^2）（２−√３＋（２＋√３）ｙ^2）^1/2

　ここで，ｙ^2＝１−ｚ^2，ｚ1^2＝１−ｙ1^2とおくと第１種楕円

　　Ｉ＝１／4√３∫(0,z1)ｄｚ／（（１−ｚ^2)（１−ｋ^2ｚ^2）^1/2＝１／4√３Ｆ（ｋ，φ1）

となる．ただし，

　　ｋ＝（√２＋√６）／４，ｋ^2＝（２＋√３）／４

　　φ1＝ａｒｃｃｏｓ（（ｃ−１＋√３）／（−ｃ＋１＋√３））＝ａｒｃｓｉｎ（（１−ｙ1^2）^1/2）

　　ｓｉｎφ1＝ｚ1，ｚ1＝（１−ｙ1^2）^1/2

　　ｃ＝１→ｚ1＝０

　　ｃ＝０→ｚ1＝（４√３−６）^1/2＝α

　これで，中間曲線の弧長を求める問題は，加法公式

　　ｚ＝｛ｘ（１＋ｍｙ^2＋ｎｙ^4）^1/2＋ｙ（１＋ｍｘ^2＋ｎｘ^4）^1/2｝／（１−ｎｘ^2ｙ^2）

　　ｍ＝−（１＋ｋ^2），ｎ＝ｋ^2，α＝（４√３−６）^1/2

の問題に還元されたことになる．

　倍角公式

　　ｘ’＝２ｘｙ／（１−ｎｘ^4）＝２ｘ（１＋ｍｘ^2＋ｎｘ^4）^1/2／（１−ｎｘ^4）

より，２等分点に対応する楕円曲線上の点

　　２ｘ（１＋ｍｘ^2＋ｎｘ^4）^1/2／（１−ｎｘ^4）＝α

の解をｘ＝βとすると，

　　１−（（ｃ−１＋√３）／（−ｃ＋１＋√３））^2＝β^2

　　ｃ＝√３＋１−２√３／（（１−β^2）^1/2＋１）

が中間曲線の２等分点である．

　ここで注意しておきたいのはｃは２等分点のｘ座標ではなく，極座標（ｒ，θ）における動径ｒであるということである．

　　ｒ^(3/2)＝ｃｏｓ（３／２θ）

　　３／２θ＝ａｒｃｃｏｓ（ｒ^3/2）

　　θ＝２ａｒｃｃｏｓ（ｒ^3/2）／３

　　ｘ＝ｒｃｏｓθ＝ｒｃｏｓ（２ａｒｃｃｏｓ（ｒ^3/2）／３）

　　ｙ＝ｒｓｉｎθ＝ｒｓｉｎ（２ａｒｃｃｏｓ（ｒ^3/2）／３）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】中間曲線のｋ等分点

　阪本ひろむ氏にMathematicaで２等分点に対応する楕円曲線上の点

　　２ｘ（１＋ｍｘ^2＋ｎｘ^4）^1/2／（１−ｎｘ^4）＝α

を求めてもらったところ，解析解

　　ｘ＝−１＋√３

が得られた．

　２等分点，４等分点，８等分点に対応する楕円曲線上の点と中間曲線上の点の数値解は以下の如くである．

　　　　　　　　　　ｘ　　　　　ｃ　　　　　　（ｘ，ｙ）

　　ｎ＝２　→　0.732051　→　0.671618　→　(0.531137,0.411053)

　　ｎ＝４　→　0.43211 　→　0.910585　→　(0.856873,0.308114)

　　ｎ＝８　→　0.226797　→　0.977135　→　(0.962279,0.169742)

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

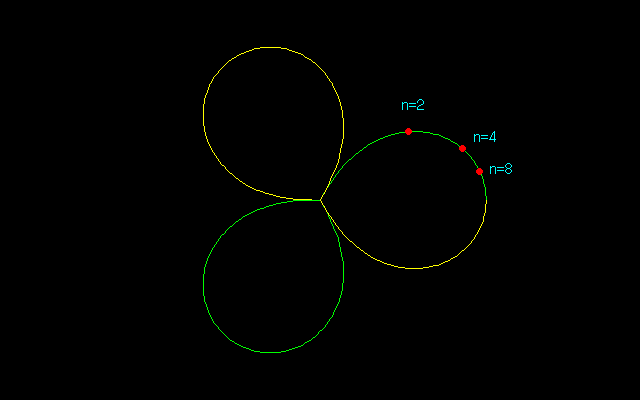
　　γ^2＝１＋ｍα^2＋ｎα^4

として，減法公式を楕円曲線：ｙ^2＝１＋ｍｘ^2＋ｎｘ^4上の点（ｘ，ｙ），（α，γ）に適用すると，反転公式は

　　ｘ’＝（γｘ−α（１＋ｍｘ^2＋ｎｘ^4）^1/2）／（１−ｎα^2ｘ^2）

で表される．

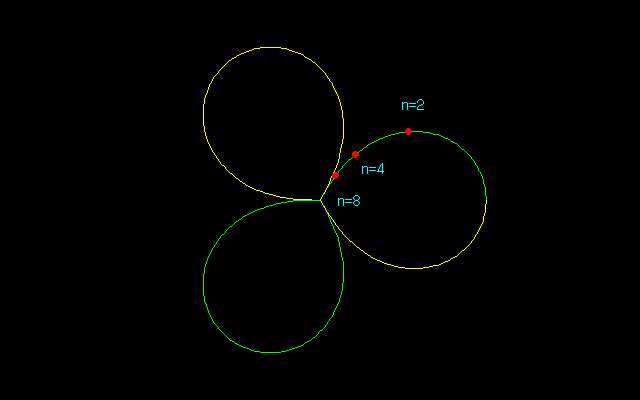
　反転先はそれぞれ

　　　　　　　　　　ｘ’　　　　ｃ　　　　　　（ｘ，ｙ）

　　ｎ＝２　→　0.732049　→　0.671621　→　(0.53114,0.411053)

　　ｎ＝４　→　0.891288　→　0.348665　→　(0.214279,0.275049)

　　ｎ＝８　→　0.934939　→　0.175156　→　(0.09489,0.147226)

に移される．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝