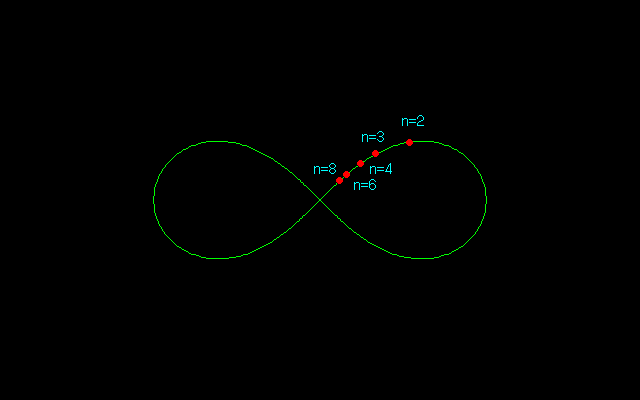
２００８年に，レムニスケートサイン関数を用いて，レムニスケートのｎ等分点を計算したが，どうしても５等分点は得られなかった．

　　　　　　　　　　ｚ　　　　（ｘ，ｙ）

　　ｎ＝２　→　0.643594　→　(0.541196,0.348311)

　　ｎ＝３　→　0.435421　→　(0.335810,0.277170)

　　ｎ＝４　→　0.327379　→　(0.243582,0.218735)

　　ｎ＝６　→　0.218456　→　(0.158115,0.150741)

　　ｎ＝８　→　0.163865　→　(0.117415,0.114304)

　そこで，

　　∫1/(1-x^4)^(1/2)dx

を，ワイエルシュトラスの標準形

　 ∫(∞,0)du/(4u^2-g2u-g3)^(1/2)

の特別な場合として扱ってみたところ，ワイエルシュトラスのペー関数を使って５等分点を得ることができた．加法定理が幾分簡単になったためである．ワイエルシュトラスのペー関数の勝利といってよいだろう．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　レムニスケートの４半弧を定規とコンパスでｎ等分できることを示すために

　　ｐ（ｎｕ）＝１

を解いて，

　　ｐ（ｕ）＝ｗ，ｚ＝１／√ｗ

とする．

　畏友・阪本ひろむ氏にお願いしてMathematicaで計算してもらったところ，解析解はとても長くなり，言葉が一切入らない数式が数ページにもおよんだ．そこで，近似解のみを示す．

　　　　　　　　　　ｚ　　　　（ｘ，ｙ）

　　ｎ＝２　→　0.643594　→　(0.541196,0.348311)

　　ｎ＝３　→　0.435421　→　(0.335810,0.277170)

　　ｎ＝４　→　0.327379　→　(0.243582,0.218735)

　　ｎ＝５　→　0.262082　→　(0.191579,0.178842)

　　ｎ＝８　→　0.163867　→　(0.117415,0.114304)

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝