（ｘ，ｙ）＝（ｆ（ｕ），ｆ’（ｕ））

とパラメトライズされる曲線について考えてみよう．もしf(u)=sin(u)ならば，x=sin(u),y=cos(u)であるから，この曲線はx^2+y^2=1（円）になる．このようにパラメトライズされる代数曲線は円だけではなく，楕円曲線もその例となっている．

　また，サイクロイド：ｘ＝ｒ（θ−ｓｉｎθ），ｙ＝ｒ（１−ｃｏｓθ）もその例である．しかし，円や楕円曲線は代数曲線であるが，サイクロイドは代数曲線ではない．サイクロイドは等分可能なのだろうか？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】サイクロイド

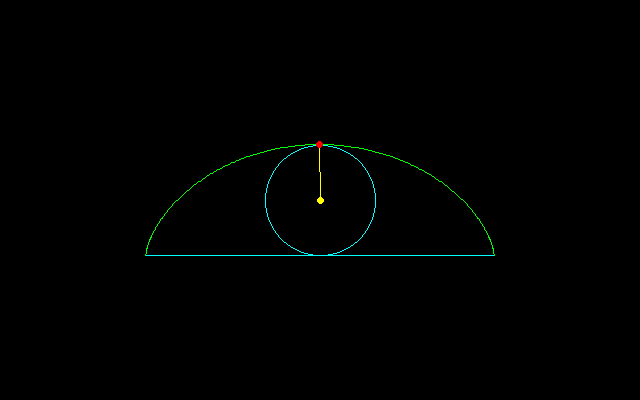
　固定した直線上を円が滑らずに転がるとき，回転円上の固定点のなす軌跡はサイクロイドと呼ばれ，回転円の半径をｒとすると

　　ｘ＝ｒ（θ−ｓｉｎθ），ｙ＝ｒ（１−ｃｏｓθ）

と書くことができます．この曲線は２変数多項式ｆ（ｘ，ｙ）＝０の形に表せませんから，代数曲線でありません．サイクロイドには

［１］最速降下線

［２］等時曲線

など，いくつかの興味深い特性があります．

　また，サイクロイド：ｘ＝ｒ（θ−ｓｉｎθ），ｙ＝ｒ（１−ｃｏｓθ）の縮閉線は

　　ｘ＝ａ（θ＋ｓｉｎθ），ｙ＝−ａ（１−ｃｏｓθ）

です．ここで，θ＝π＋ｔとおけば

　　ｘ＝ａ（ｔ−ｓｉｎｔ）＋ａπ，ｙ＝ａ（１−ｃｏｓｔ）−２ａ

ですから，もとのサイクロイドと合同なサイクロイドになることが示されます．（なお，対数らせんの伸開線もそれと合同な対数らせんになる．）

　サイクロイドはそもそもガリレイによって発見され，ホイヘンスによって振子時計の設計に使われ，そしてパスカルの積分法の研究にも貢献しています．サイクロイド弧が囲む面積は３πｒ^2（回転円の面積の３倍に等しい），弧長は８ｒ（回転円に外接する正方形の周に等しい）になります．

［１］面積

　　∫(0,2π)ｙｄｘ＝ｒ^2∫(0,2π)（１−ｃｏｓｔ）^2ｄｔ

　＝ｒ^2［ｔ−２ｓｉｎｔ＋ｔ／２＋ｓｉｎ２ｔ／４］＝３πｒ^2

［２］弧長

　　∫(0,2π)（ｘ’^2＋ｙ’^2）^1/2ｄｔ＝∫(0,2π)（ｙ^2＋ｙ’^2）^1/2ｄｔ

　＝√２ｒ∫（１−ｃｏｓｔ）^1/2ｄｔ＝２ｒ∫ｓｉｎ（ｔ／２）ｄｔ

　＝２ｒ［−２ｃｏｓ（ｔ／２）］＝８ｒ

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】サイクロイド弧長のｎ等分

　　２ｒ（−２ｃｏｓ（ｔ／２）＋２）＝８ｒ／ｎ

　　−２ｃｏｓ（ｔ／２）＋２＝４／ｎ

　　ｃｏｓ（ｔ／２）＝１−２／ｎ

ｔが４直角の整数分の１になるのは，ｎ＝２とｎ＝４のときのみです．

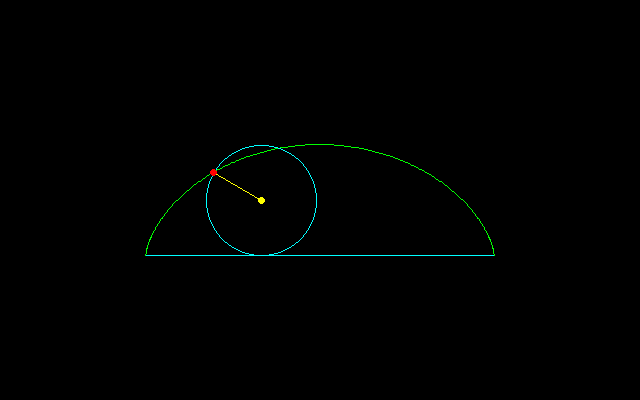
［１］ｎ＝２のとき，ｔ／２＝π／２→ｔ＝π（ｙ＝２ｒ）

［２］ｎ＝４のとき，ｔ／２＝π／３→ｔ＝２π／３（ｙ＝３ｒ／２）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝