レムニスケートといえば，一般にベルヌーイのレムニスケートを指す場合が多いが，もともと８の字曲線を表す用語であり，Geronoのレムニスケート，Boothのレムニスケート，Montferrierのレムニスケート，Slueseのレムニスケートなど多くのレムニスケートがあるそうだ．

　ベルヌーイのレムニスケート：

　　直交座標：（ｘ^2＋ｙ^2）^2＝（ｘ^2−ｙ^2）

　　極座標　：ｒ^2 ＝ｃｏｓ２θ

は数学史上重要な意義を果たした４次曲線であるが，三角関数を用いて

　　ｘ＝ｃｏｓθ／（１＋ｓｉｎ^2θ）

　　ｙ＝ｓｉｎθｃｏｓθ／（１＋ｓｉｎ^2θ）

ここで，

ｓｉｎθ＝（１−ｔ^2）／（１＋ｔ^2）

ｃｏｓθ＝２ｔ／（１＋ｔ^2）

とおくと，

　　ｘ＝ｔ（１＋ｔ^2）／（１＋ｔ^4 ）

　　ｙ＝ｔ（１−ｔ^2）／（１＋ｔ^4 ）

のようにパラメトライズされる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】ベルヌーイのレムニスケートのｎ等分点

　ベルヌーイのレムニスケートの方程式は

　　（ｘ^2＋ｙ^2）^2＝ｘ^2−ｙ^2

である．

　第１象限にある部分だけを考えることにして，この弧は原点Ｏ（０，０）を始点，Ｐ（１，０）を終点としてパラメータｚ（０≦ｚ≦１）を用いれば，

　　ｘ^2＝１／２（ｚ^2＋ｚ^4），ｙ^2＝１／２（ｚ^2−ｚ^4）

と表せる．

　この線素は

　　ｄｓ＝（ｄｘ^2＋ｄｙ^2）^1/2＝ｄｚ／（１−ｚ^4）^1/2

で与えられ，倍角公式

　　ｚ→２ｚ（１−ｚ^4）^1/2／（１＋ｚ^4）

はｄｓを２ｄｓに変える．

　　２ｚ（１−ｚ^4）^1/2／（１＋ｚ^4）＝１

と置くことによって

　　ｚ^2＝√２−１

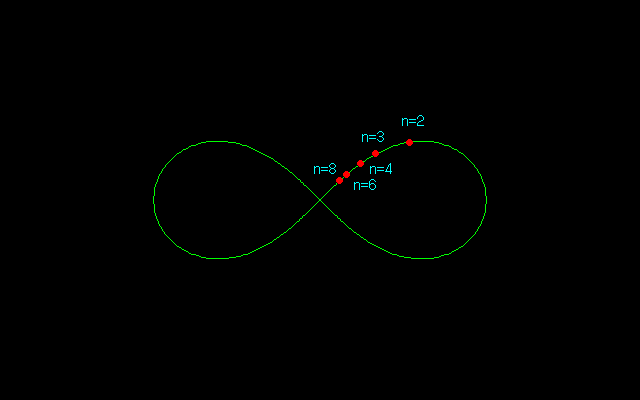
が得られる．以上より，

　　　　　　　　　　ｚ　　　　（ｘ，ｙ）

　　ｎ＝２　→　0.643594　→　(0.541196,0.348311)

　　ｎ＝３　→　0.435421　→　(0.335810,0.277170)

　　ｎ＝４　→　0.327379　→　(0.243582,0.218735)

　　ｎ＝６　→　0.218456　→　(0.158115,0.150741)

　　ｎ＝８　→　0.163865　→　(0.117415,0.114304)

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】リンク装置の機構学

　複数の棒を互いに結合してできる連接棒を「リンク装置」と呼びます．連接棒の一点を直線や曲線に沿って動かすとき，複雑な変化のある曲線を描くことができます．リンク装置の用途は多方面にわたり，角の３等分問題や立方体倍積問題を解くのにも使われます．

　パンタグラフのようなリンク装置利用すると拡大・縮小が可能になりますが，たとえば，円錐曲線をすべて描けないかという発想も生まれてきます．

　　［参］礒田正美編「曲線の事典」，共立出版

によれば，リンク装置の一点を直線に沿って動かすとき，与えられた直線が３本ないし４本の場合に円錐曲線を作図できるそうです．

　ユークリッドが考察していたとされ，アポロニウスが取り上げ，パップスが成果をあげた難題に三線問題，四線問題があります．

ａ）三線問題：ひとつの直線への距離の平方が，ほかの２直線への距離の積に対して与えられた比をもつ点の軌跡を求める問題

ｂ）四線問題：１組の直線への距離の積が，ほかの２直線への距離の積に対して与えられた比をもつ点の軌跡を求める問題

　このような点の軌跡は円錐曲線となります．デカルトはｎ本の直線の場合に一般化し，完全な解答を与えました．すなわち，３本ないし４本の直線が与えられたときには２次になり，５本ないし６本（五線問題，六線問題）では３次になり，直線が２本加わるたびに次数が１次増加します．

　２次曲線のみならず高次曲線作図器も製作されていて，たとえば，ベルヌーイのレムニスケートは単純なリンク装置を使って描くことができます．これはワットの蒸気機関に応用されています．また，ポースリエの反転器は円運動を直線運動に，直線運動を円運動に変換する機構で，リンク装置の用途は多方面にわたっています．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【３】レムニスケートのリンク装置

　２つのピン止めされた固定関節は半径Ｒが同じ２つの異なる円の中心（ａ，０），（−ａ，０）であり，また，２つの自由関節はそれぞれの円の円周上を自由に動きます．２つのピン止めされた固定関節間距離は２ａで中央のバーの長さと同じ，Ｒはその１／√２倍で，Ｒ＝ａ√２です．

　このとき，中央のバー（長さ２ａ）の中点は８の字型曲線

　　ｒ^2＝２ａ^2ｃｏｓ２ｔ

を描きます．

　ところで，

　　左の回転軸の位相をθ→（Ｒｃｏｓθ−ａ，Ｒｓｉｎθ）

　　右の回転軸の位相をφ→（Ｒｃｏｓφ＋ａ，Ｒｓｉｎφ）

　　回転軸間の距離→２ａ

となることから，

　　（Ｒｃｏｓφ−Ｒｃｏｓθ＋２ａ）^2＋（Ｒｓｉｎφ−Ｒｓｉｎθ）^2＝（２ａ）^2

　　ｃｏｓ（φ−θ）＝√２（ｃｏｓφ−ｃｏｓθ）＋１

　　１−２ｓｉｎ^2（φ−θ）／２＝−√２ｓｉｎ（φ＋θ）／２ｓｉｎ（φ−θ）／２＋１

　　√２ｓｉｎ（φ−θ）／２＝ｓｉｎ（φ＋θ）／２

となって，φとθの非線形関係がわかるだけです．

　そこで，（Ｒｃｏｓθ−ａ，Ｒｓｉｎθ）と（ａ，０）を結ぶ直線とｘ軸とのなす角度をαとして，交叉平行四辺形であることより

　　０＜θ＜π→　φ＝θ＋２α

　　π＜θ＜２π→φ＝θ−２α

として，φを求めます．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝