ガウスの円周等分理論「コンパスと定規でｎ等分できるのは，２^2^qi＋１の形をした相異なる素数ｐiにより２^mΠｐiと書かれる場合である」は円関数ばかりでなく他の超越関数，たとえば，

　　u=∫(0,x)f(t)=1/(1-t^4)^(1/2)dt

にも応用できる．（その４０）を補足しておきたい．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】レムニスケートのｎ等分点

　レムニスケートサインはレムニスケートｒ^2＝ｃｏｓ２θ（あるいはｒ^2＝ｓｉｎ２θ）の弧長を表す積分の逆関数

　　∫(0,x)1/(1-t^4)^(1/2)dt

として定義される．

　　ω=∫(0,1)1/(1-t^4)^(1/2)dt

はレムニスケート全体の長さの１／４である．

　ファニャーノはレムニスケートの和公式

　　ｚ＝｛ｘ（１−ｙ^4）^1/2＋ｙ（１−ｘ^4）^1/2｝／（１＋ｘ^2ｙ^2）

を得て，レムニスケートを２，３，５等分する点の座標を求める代数的な計算公式を見いだした．

　レムニスケートの線素は

　　ｄｓ＝（ｄｘ^2＋ｄｙ^2）^1/2＝ｄｚ／（１−ｚ^4）^1/2

で与えられ，倍角公式

　　ｚ→２ｚ（１−ｚ^4）^1/2／（１＋ｚ^4）

はｄｓを２ｄｓに変える．

　　２ｚ（１−ｚ^4）^1/2／（１＋ｚ^4）＝１

と置くことによって

　　ｚ^2＝√２−１

が得られる．実際に計算してみると，レムニスケート弧長の２等分点は

　　sl(u/2)=(-1+√2)^1/2=0.643594

３等分点は

　　sl(u/3)=1/2(1-(√2)(3)^1/4+√3)=0.435421

で示される．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】極座標から直交座標へ

　ベルヌーイのレムニスケートの方程式は

　　（ｘ^2＋ｙ^2）^2＝ｘ^2−ｙ^2

である．

　第１象限にある部分だけを考えることにして，この弧は原点Ｏ（０，０）を始点，Ｐ（１，０）を終点としてパラメータｚ（０≦ｚ≦１）を用いれば，

　　ｘ^2＝１／２（ｚ^2＋ｚ^4），ｙ^2＝１／２（ｚ^2−ｚ^4）

と表せる．

　ここで注意しておきたいのはｚは極座標（ｒ，θ）における動径ｒであるということである．レムニスケートの場合，

　　ｒ^2＝ｃｏｓ２θ＝２ｃｏｓ^2θ−１＝１／２ｓｉｎ^2θ

より，

　　ｃｏｓθ＝（（１＋ｒ^2）／２）^1/2

　　ｓｉｎθ＝（（１−ｒ^2）／２）^1/2

したがって，

　　ｘ＝ｒｃｏｓθ＝（（ｒ^2＋ｒ^4）／２）^1/2

　　ｙ＝ｒｓｉｎθ＝（（ｒ^2−ｒ^4）／２）^1/2

　あるいは

　　ｚ^2＝ｘ^2＋ｙ^2

　　ｚ^4＝ｘ^2−ｙ^2

より

　　ｘ^2＝１／２（ｚ^2＋ｚ^4），ｙ^2＝１／２（ｚ^2−ｚ^4）

　したがって，レムニスケートの２等分点を求める際，

　　ｓｌ（２ｚ）＝２ｚ（１−ｚ^4）^1/2／（１＋ｚ^4）＝１

とおいてｚを求めたあと，

　　ｘ^2＝１／２（ｚ^2＋ｚ^4），ｙ^2＝１／２（ｚ^2−ｚ^4）

により，２等分点（ｘ，ｙ）を求めなければならないことになる．

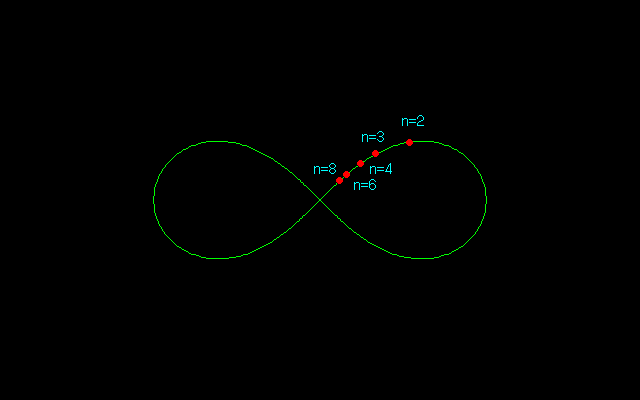
　　　　　　　　　　ｚ　　　　（ｘ，ｙ）

　　ｎ＝２　→　0.643594　→　(0.541196,0.348311)

　　ｎ＝３　→　0.435421　→　(0.335810,0.277170)

　　ｎ＝４　→　0.327379　→　(0.243582,0.218735)

　　ｎ＝６　→　0.218456　→　(0.158115,0.150741)

　　ｎ＝８　→　0.163865　→　(0.117415,0.114304)

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝