ポンスレーの定理と解析幾何学を用いると
R^2−2Rr=d^2 (オイラーの定理)
2r^2(R^2+d^2)=(R^2−d^2)^2 (フースの定理)
は大学入試程度の問題に還元できることがわかった.
フースは双心五角形,六角形,七角形,八角形に関する同様の公式も見つけたとされているが,数式処理ソフトを利用しても双心八角形の基底はまだ得られていない.
フースの論文(Nova Acta Petropol XIII, 1798)を入手するのは難しそうであるが,彼は本当に基底を見つけたのだろうか? 計算方法を与える方程式を示しただけではなかろうかと思われるのである.
===================================
【1】レムニスケート弧長のn等分
たとえば,レムニスケートサインの半角公式
sl(u/2)=(-1+√2)^1/2
は四則演算および平方根により得られますので,円同様,レムニスケートの4半弧も定規とコンパスだけで弧長を1/2倍にする作図が可能であることが示される.
レムニスケート(連珠形)には円に共通する性質があり,定規とコンパスだけで奇数のn等分することができる必要十分条件はnがフェルマー素数(n=22^m+1の形の素数:3,5,17,257,65537)であることはよく知られている.
ファニャーノは倍角公式,4倍角公式によって得られるものに置き換えて,レムニスケートの四半弧の3等分あるいは5等分を与える代数方程式を導いたとされている.
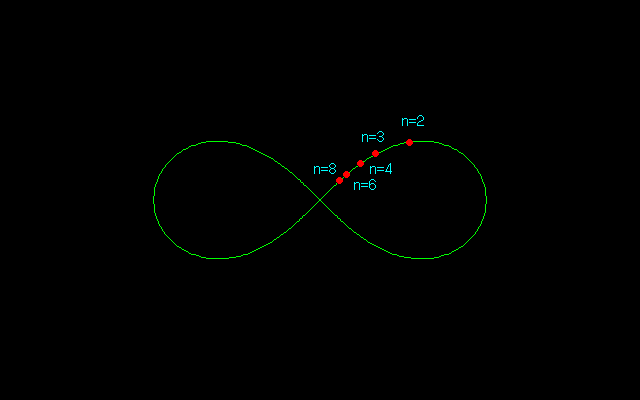
レムニスケート弧長のn等分点を求めるには,sl(nu)=1として方程式を解いてsl(u)の値を求めることになるのだが,そうなると手計算では到底太刀打ちできない.よほど筆算が好きな計算マニアであっても,この計算は筆算ではもはや不可能である.2,3等分点は求められたものの,どうしても5等分点は得られなかった.

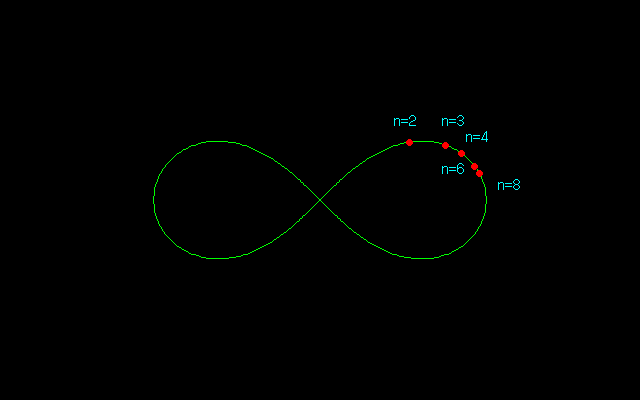
おそらくファニャーノはレムニスケート弧長の3等分あるいは5等分を与える代数方程式を導いただけで,解を示すことはできなかったと思われる.
===================================
【2】レムニスケート積分の倍角公式
ベルヌーイはレムニスケートの弧長を
f(x)=1/(1-x^4)^(1/2)
u=F(x)=∫(0,x)f(t)dt
と表しました.これがレムニスケート積分と呼ばれる典型的な楕円積分です.また,
∫(0,1)f(t)dt=1.311028・・・=ω
とおくと,4ωがレムニスケートの全長になります.円に類比すると,レムニスケートの定数(レムニスケート周率)ωは円に対する円周率πと同じ役割を演じていることになります.
F(x)の逆関数であるレムニスケートサインsl(u)も周期4ωをもつことがわかります.レムニスケートサインを求めてみることにしましょう.実際に1/(1-x^4)^(1/2)を2項展開し,さらに項別積分すると
F(x)=x+1/10x^5+1/24x^9+5/208x^16+・・・
この逆関数のべき級数展開は
sl(u)=u-1/10u^5+1/120u^9+11/15600u^13+・・・
=u(1-1/10u^4+1/120u^8+・・・)
=ug(u^4)
となります.
円積分では
x=sinu,f'(u)=dx/du=1/du/dx=(1-x^2)^1/2=y(=cosu=sin'u)
よりx,yはともにパラメータuの関数になりましたが,レムニスケート積分でもx=sl(u),y=sl'(u)はともにパラメータuの関数になり,曲線y^2=1−x^4はx=sl(u),y=sl'(u)によってパラメータ表示できます.
ここで,sl(2u)をsl(u)の関数として表せればよいことになるのですが,レムニスケートサインの倍角の公式(あるいは加法定理)は
sl(u+v)=(sl(u)sl'(v)+sl(v)sl'(u))/(1+sl^2(u)sl^2(v))
sl(2u)=2sl(u)sl'(u)/(1+sl^4(u))
sl'(u)=(1-sl^4(u))^1/2
sl(2u)=2sl(u)(1-sl^4(u))^1/2/(1+sl^4(u))=2x(1-x^4)^1/2/(1+x^4)
のようになります.レムニスケートサインとその導関数が正弦関数とその導関数である余弦関数にいかに類似しているかわかるでしょう.
2u=sl^(-1)(2x(1-x^2)^1/2/(1+x^4))
したがって,レムニスケート積分の倍角公式(ファニャーノの倍角公式)
2∫(0,x)f(t)dt=∫(0,2x(1-x^4)^1/2/(1+x^4))f(t)dt
2G(x)=G(2x(1−x^4)^1/2/(1+x^4))
が成り立ちます.
2x(1-x^4)^1/2/(1+x^4)もxから四則演算および平方根により得られますので,円同様,レムニスケートも定規とコンパスだけで弧長を2倍にする作図が可能であることを示しています.
1751年,オイラーは逆正弦関数の加法定理
G(x)+G(y)=G(x(1−y^2)^1/2+y(1−x^2)^1/2)
との類似に基づいて,レムニスケート積分に対する加法定理
G(x)+G(y)=G((x(1−y^4)^1/2+y(1−x^4)^1/2))/(1+x^2y^2))
を構成することに成功しています.
===================================
【3】レムニスケートサインのn倍角公式
レムニスケートサインの加法定理
sl(u+v)=(sl(u)sl'(v)+sl(v)sl'(u))/(1+sl^2(u)sl^2(v))
より,
sl(2u)=2sl(u)sl'(u)/(1+sl^4(u))
sl(3u)=(sl(2u)sl'(u)+sl(u)sl'(2u))/(1+sl^2(2u)sl^2(u))
sl(4u)=(sl(3u)sl'(u)+sl(u)sl'(3u))/(1+sl^2(3u)sl^2(u))
sl(5u)=(sl(4u)sl'(u)+sl(u)sl'(4u))/(1+sl^2(4u)sl^2(u))
sl(6u)=(sl(5u)sl'(u)+sl(u)sl'(5u))/(1+sl^2(5u)sl^2(u))
また,
sl'(u)=(1-sl^4(u))^1/2
sl'(2u)=(1-sl^4(2u))^1/2
sl'(3u)=(1-sl^4(3u))^1/2
sl'(4u)=(1-sl^4(4u))^1/2
sl'(5u)=(1-sl^4(5u))^1/2
を用いて,sl(u)の関数として表すと
sl(2u)=2sl(u)(1-sl^4(u))^1/2/(1+sl^4(u))
などが得られます.
しかし,sl(nu),n≧3をsl(u)の関数として表すことは大層複雑であって,手計算を断念せざるを得ませんでした.そこで,畏友・阪本ひろむ氏にお願いしてMathematicaで展開してもらったところ,言葉が一切入らない数式が数ページにもおよびました.
===================================