
[定理]単位円に内接する正n角形のひとつの頂点から他のn−1個の頂点までの距離の積はnに等しい.
=[定理]単位円に内接する正n角形のすべての2頂点間の距離の積はn^n/2に等しい.
また,
[定理]単位円に内接する正n角形のすべての2頂点間の距離の平方和はn^2に等しい
=[定理]単位円に内接する正n角形のひとつの頂点から他のn−1個の頂点までの距離の平方和は2nに等しい.
いずれの定理を用いたとしても,単位円に内接する正三角形の1辺の長さは√3になることがわかるだろう.
(その1)では
(Q)中心O,半径rの円の内部に任意の点Pをとるとき,
OP<r/2
である確率はいくらか?
を考えたが,(その2)における考察は
(Q)直線が円によって切り取られるときの弦の長さが,円に内接する正三角形の1辺の長さより長くなる確率はいくらか?
というもので,
(A1)円の中心から下ろした垂線の足が,円の内部に一様分布する.そのとき,条件を満たすためには,垂線の足が円の半径の1/2の同心円の内部に存在しなければならないので1/4.

(A2)円のひとつの直径上で一様分布し,直線の方向はこれとは独立に一様分布する.そのとき,条件を満たすためには,円の中心から半径の1/2の距離の内部を通らなければならないので1/2.
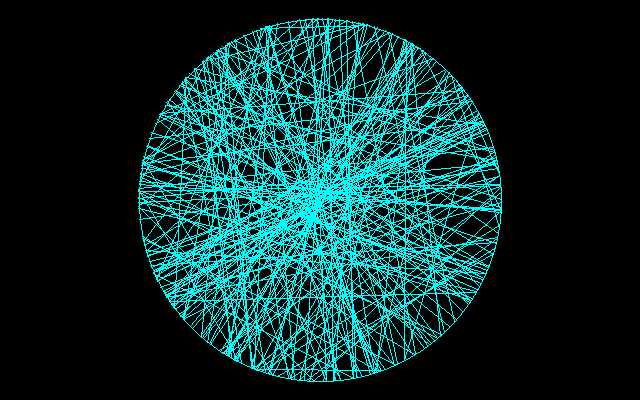
(A3)2点が円周上で一様分布する.このときひとつの交点は固定でき,他の交点が条件を満たす場所に存在する確率は1/3.

===================================
プログラムを掲げておく.
1000 '
1010 ' **** Bertrand ****
1020 ' 2011/10/11 (C) サトウ イクロウ
1030 SCREEN 3,0:CONSOLE ,,0,1
1040 CLS 3:WIDTH 80,25:COLOR 6
1050 PI=3.14159
1060 '
1070 CLS 3
1080 WW=11:R=10
1090 WINDOW(-WW,-WW)-(WW,WW)
1100 VIEW(120,0)-(519,399)
1110 '
1120 ' [A1]
1130 X1=0:Y1=0
1140 CIRCLE(X1,-Y1),R,5
1150 '
1160 ICNT=0
1170 WHILE ICNT<200
1180 R1=RND(1):R2=RND(2)
1190 X1=(2*R1-1)*R:Y1=(2*R2-1)*R :IF (X1*X1+Y1*Y1)>R*R THEN 1180
1200 M=-X1/Y1
1210 A=1+M*M:B=-2*M*M*X1+2*M*Y1:C=M*M*X1*X1-2*M*X1*Y1+Y1*Y1-R*R
1220 X2=(-B+SQR(B*B-4*A*C))/2/A:Y2=M*(X2-X1)+Y1
1230 X3=(-B-SQR(B*B-4*A*C))/2/A:Y3=M*(X3-X1)+Y1
1240 LINE(X2,-Y2)-(X3,-Y3),5
1250 ICNT=ICNT+1
1260 WEND
1270 STOP
1280 'FL$="c:\bmp\1733_1":GOSUB *GSAVE
1290 '
1300 ' [A2]
1310 CLS 3
1320 X1=0:Y1=0
1330 CIRCLE(X1,-Y1),R,5
1340 '
1350 ICNT=0
1360 WHILE ICNT<200
1370 R1=RND(1)*2-1:R2=RND(2):R3=RND(3)
1380 X1=R1*COS(2*PI*R2)*R:Y1=R1*SIN(2*PI*R2)*R:M=TAN(2*PI*R3)
1390 A=1+M*M:B=-2*M*M*X1+2*M*Y1:C=M*M*X1*X1-2*M*X1*Y1+Y1*Y1-R*R
1400 X2=(-B+SQR(B*B-4*A*C))/2/A:Y2=M*(X2-X1)+Y1
1410 X3=(-B-SQR(B*B-4*A*C))/2/A:Y3=M*(X3-X1)+Y1
1420 LINE(X2,-Y2)-(X3,-Y3),5
1430 ICNT=ICNT+1
1440 WEND
1450 STOP
1460 'FL$="c:\bmp\1733_2":GOSUB *GSAVE
1470 '
1480 ' [A3]
1490 CLS 3
1500 X1=0:Y1=0
1510 CIRCLE(X1,-Y1),R,5
1520 '
1530 ICNT=0
1540 WHILE ICNT<200
1550 R1=RND(1):R2=RND(2)
1560 X1=COS(2*PI*R1)*R:Y1=SIN(2*PI*R1)*R
1570 X2=COS(2*PI*R2)*R:Y2=SIN(2*PI*R2)*R
1580 LINE(X1,-Y1)-(X2,-Y2),5
1590 ICNT=ICNT+1
1600 WEND
1610 STOP
1620 'FL$="c:\bmp\1733_3":GOSUB *GSAVE
1630 '
1640 WINDOW(0,0)-(639,399)
1650 VIEW(0,0)-(639,399)
1660 '
1670 GOSUB *TEMP
1680 SCREEN 3,0:CLS 3
1690 END
1700 '
1710 *TEMP:
1720 LOCATE 0,0 :PRINT "何かキーを押してください";:WHILE INKEY$="":WEND
1730 RETURN
1740 '
1750 ' ** VRAM SAVE **
1760 '
1770 *GSAVE:
1780 DEF SEG=&HA000
1790 BSAVE FL$+".CHR",&H0,&HFA0
1800 DEF SEG=&HA200
1810 BSAVE FL$+".ATR",&H0,&HFA0
1820 DEF SEG=&HA800
1830 BSAVE FL$+".BLU",&H0,&H7D00
1840 DEF SEG=&HB000
1850 BSAVE FL$+".RED",&H0,&H7D00
1860 DEF SEG=&HB800
1870 BSAVE FL$+".GRN",&H0,&H7D00
1880 RETURN
===================================