【１】三角形の重心

　三角形の３つの中線は一点で交わります．この交点が三角形の重心です．原点Ｏに対する三角形ＡＢＣの３頂点Ａ，Ｂ，Ｃの位置ベクトルをそれぞれａ，ｂ，ｃとすれば，重心の位置ベクトルは（ａ＋ｂ＋ｃ）／３となります．三角形の形をした均一な板の重心は３つの中線の交点，すなわち重心にあります．この点（一様な三角形の重心）は３つの頂点の重心（ａ＋ｂ＋ｃ）／３，すなわち三角形の頂点におかれた３つの等しい質量の中心（物理的重心）に一致します．また，重心は３頂点に至る距離の２乗の和が最小となる点です．

　三角形の辺の中点同士を結ぶと互いの合同な４つの三角形に分割されます．この小さい三角形（中点三角形）の面積はもとの三角形の面積の１／４，周長は１／２に等しくなります．また，中点三角形の重心はもとの三角形の重心と一致します．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】ヴァリニョンの平行四辺形

　四角形の中点を結んでできる四角形は平行四辺形である．この小さい平行四辺形の面積はもとの四角形の面積の１／２，周長は対角線の長さの和に等しい．四角形を対角線で２つの三角形に分け，中点連結定理を適用すればこのことがわかる．

　したがって，四角形の対辺の中点を結ぶ線分は互いに他を２等分することもわかる．

　この小さい平行四辺形の面積はもとの四角形の面積の１／２，周長は対角線の長さの和に等しい．それでは，また，四角形の４つの頂点に同じ質量を置いたときの重心は中点線の交点（ヴァリニョンの平行四辺形の中心）

　　（ａ＋ｂ＋ｃ＋ｄ）／４

に一致する．同じ操作を次々に繰り返すと一連の平行四辺形ができるが，それらの重心ももとの四角形の重心と一致する．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【３】ウィッテンバウアーの平行四辺形

　もとの四角形の各辺の３等分点をとり，隣り合った３等分点を結ぶと８角形になるが，この線分の延長上にできる交点を結んでも平行四辺形ができる．この平行四辺形はウィッテンバウアーの平行四辺形と呼ばれる．

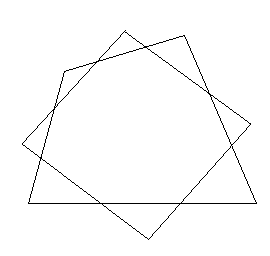
　もとの四角形の重心はウィッテンバウアーの平行四辺形の中心と一致する．

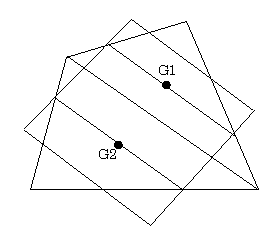
（証）四角形を対角線で２つの三角形に分けると，三角形の重心はもとの四角形とウィッテンバウアーの平行四辺形の交点を結ぶ線分の中点となる．したがって，もとの四角形の重心はウィッテンバウアーの平行四辺形の対辺の中点を結ぶ直線上にあることがわかる．同様に，もうひとつの対角線で２つの三角形に分けると，もとの四角形の重心はウィッテンバウアーの平行四辺形の中心と一致することが結論される．

　ウィッテンバウアーの平行四辺形の面積はもとの四角形の面積の８／９，周長は対角線の長さの４／３に等しい．また，もとの四角形とウィッテンバウアーの平行四辺形が重なった部分の８角形の面積はもとの四角形の面積の７／９，ウィッテンバウアーの平行四辺形の面積の７／８に等しい．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【４】円周四角形の角の２等分

　円周四角形の各角の２等分線は円周と交わる４点は長方形をなす（円周四角形の対角線が直交すれば，正方形になる）．

　三角形の内角の３等分線の交点は正三角形になるという．モーレーの三角形がわずか１００年前に発見されたというのは驚きである．そこで円周四辺形でも試してみることもできるだろう（練習問題とする）．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝