円周を１２等分する点が与えられているとき，３点を結んでできる直角三角形は３：４：５のものだけである（総数は６０個）．

（証）無限に多く存在するピタゴラス数（ａ^2＋ｂ^2＝ｃ^2）はすべて

　　ａ＝ｋ（ｘ^2−ｙ^2），ｂ＝２ｋｘｙ，ｃ＝ｋ（ｘ^2＋ｙ^2）

で生成される（１≦ｙ＜ｘ）．

　　ｘ^2−ｙ^2＋２ｘｙ＋ｘ^2＋ｙ^2＝２ｘ（ｘ＋ｙ）≦１２

　　ｘ（ｘ＋ｙ）≦６よりｘ＝２，ｙ＝１　→　ｘ^2＋ｙ^2＝５

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】音学における３：４：５定理

　三平方の定理をみつけたのはピタゴラスですが，音階（ドレミファソラシド）を初めて作ったのもピタゴラスです．（現在使われている音階はピタゴラスの音階を改良した１２平均律音階です．半音上がるごとに振動数が２^1/12倍になります．）

　ところで，円周を１２等分する点に１２音階ドド＃レミｂミファファ＃ソソ＃ラシｂシを時計回りに配置します．このとき，たとえばドミソはミはドから４つ目の音，ソはミから３つ目の音，またソから時計回りに数えるとドは５つ目の音になっています．

　和音ドミソは４−３−５の関係にあるわけです．和音は調和した美しい響きになりますが，ドミソに限らずファラド，ソシレなども４−３−５の関係にあります．反時計回りも含め，円周を３：４：５または４：３：５に分割する直角三角形の総数は６０個あります．ピタゴラスの定理が和音にも関係してくるのはとても不思議な気がします．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】数楽における３：４：５定理

　平行四辺形の頂点Ａ，Ｂ，Ｃ，Ｄをそれぞれ辺ＢＣ，ＣＤ，ＤＡ，ＡＢの中点と結んで，中央に小さい平行四辺形を作る．この小さい平行四辺形の面積は，もとの平行四辺形の面積の１／５に等しい．次に，平行四辺形の頂点Ａ，Ｂ，Ｃ，Ｄをそれぞれ辺ＣＤ，ＤＡ，ＡＢ，ＢＣの中点と結んでも中央に小さい平行四辺形が得られる．この小さい平行四辺形が重なった部分は点対称な８角形で，その面積はもとの平行四辺形の面積の１／６に等しい．

　このとき，重なっている小さい平行四辺形は互いの辺を３等分するのではなく，辺を分割する比は４：５：３になっている．

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

　平行四辺形の頂点と２等分点を使ったダイヤグラムでは，平行四辺形の重なりにおいて，４：５：３の比があらわれた．では，３等分点を使ったダイヤグラムではどうだろうか？

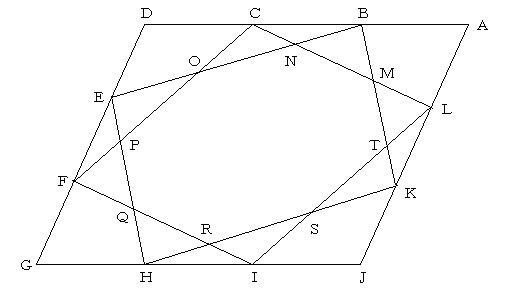
　求めるのは，ＥＯ：ＯＮ：ＮＢであるが，４：５：３になっていることが証明される．平行四辺形の辺を３等分すると「３：４：５定理」が得られるのであるが，こんなところにも直角三角形に関係する３：４：５があるのかと驚かされた．辺分割の仕方によってはたとえば「７：５：３定理」であったり「α：β：γ定理」であったり，自分なりの定理が見つかるのではないかと思う．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝