中川宏さんは，三角形で得られた結果を平行四辺形の場合に拡張してみたのであるが，今回のコラムではその結果を紹介したい．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

［１］平行四辺形の角の２等分

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

［２］平行四辺形の角の３等分

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

［３］平行四辺形の辺の２等分

　平行四辺形の頂点Ａ，Ｂ，Ｃ，Ｄをそれぞれ辺ＢＣ，ＣＤ，ＤＡ，ＡＢの中点と結んで，中央に小さい平行四辺形を作る．この小さい平行四辺形の面積は，もとの平行四辺形の面積の１／５に等しい．

　一般に与えられた平行四辺形の各辺を同じ倍率ｋで伸縮した位置に点をとって作った四角形の面積は，もとの平行四辺形の面積の

　　Ｍ＝２ｋ^2−２ｋ＋１＝２（ｋ−１／２）^2＋１／２

倍になる．

　　ｋ＝１／３　→　Ｍ＝５／９

　　ｋ＝１／２　→　Ｍ＝１／２

　　ｋ＝２／３　→　Ｍ＝５／９

　　ｋ＝１　　　→　Ｍ＝１

　　ｋ＝３／２　→　Ｍ＝５／２

　　ｋ＝２　　　→　Ｍ＝５

０＜ｋ＜１のときはもとの平行四辺形より小さくなり，ｋ＝１／２のとき最小値１／４をとる．ｋ＞１のときはもと平行四辺形より大きくなり，ｋ＝３／２のときには５／２倍になるが，与えられた平行四辺形の各辺を逆方向に延ばすと大きな平行四辺形の対辺を１：２に内分する点と交わるのである．

　次に，平行四辺形の頂点Ａ，Ｂ，Ｃ，Ｄをそれぞれ辺ＣＤ，ＤＡ，ＡＢ，ＢＣの中点と結んでも中央に小さい平行四辺形が得られる．この小さい平行四辺形が重なった部分は点対称な８角形で，その面積はもとの平行四辺形の面積の１／６に等しい．

　このとき，重なっている小さい平行四辺形は互いの辺を３等分するのではなく，辺を分割する比は４：５：３になっている．

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

［４］平行四辺形の辺の３等分

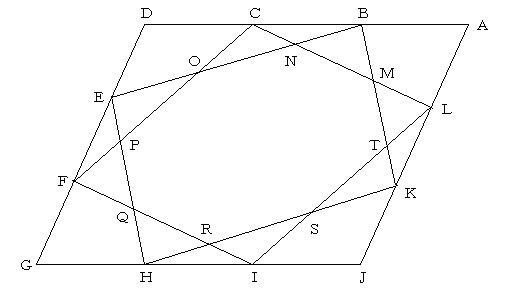
　平行四辺形の頂点と２等分点を使ったダイヤグラムでは，平行四辺形の重なりにおいて，４：５：３の比があらわれた．では，３等分点を使ったダイヤグラムではどうだろうか？　ここでも，ＥＯ：ＯＮ：ＮＢ＝４：５：３である．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝