【１】ヴァリニョンの平行四辺形

　四角形の中点を結んでできる四角形は平行四辺形である．この小さい平行四辺形の面積はもとの四角形の面積の１／２，周長は対角線の長さの和に等しい．四角形を対角線で２つの三角形に分け，中点連結定理を適用すればこのことがわかる．

　したがって，四角形の対辺の中点を結ぶ線分は互いに他を２等分することもわかる．

　四角形の４つの頂点に同じ質量をを置いたときの重心は中点線の交点（ヴァリニョンの平行四辺形の中心）

　　（ａ＋ｂ＋ｃ＋ｄ）／４

に一致する．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】ウィッテンバウアーの平行四辺形

　それに対して，四角形状の薄板の重心

ｇ＝｛（２□−△ＢＣＤ）ａ＋（２□−△ＣＤＡ）ｂ＋（２□−△ＤＡＢ）ｃ＋（２□−△ＡＢＣ）ｄ｝／６□

　＝（ａ＋ｂ＋ｃ＋ｄ）／３−｛△ＢＣＤ・ａ＋△ＣＤＡ・ｂ＋△ＤＡＢ・ｃ＋△ＡＢＣ・ｄ｝／６□

は，ウィッテンバウアーの平行四辺形の中心に一致する．

　ウィッテンバウアーの平行四辺形とは，四角形の各辺の３等分点をとり，隣り合った等分点を結ぶと平行四辺形ができるが，四角形の重心Ｇはその平行四辺形の中心と一致するというわけである．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
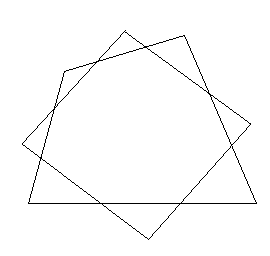
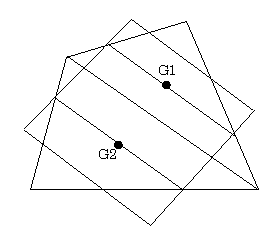