三角形は３辺に平行な等分線を引くことによって，ｎ^2個に相似分割できるが，中線に平行な等分線を引くことによっても相似分割することが出来る．このような分割は何等分だろうか？　　　（中川宏）

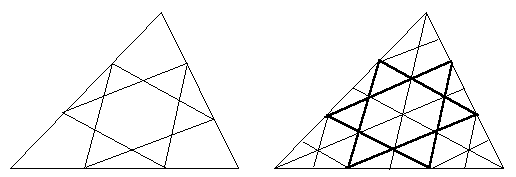
［証］各辺を２ｎ等分した場合，着色した完全な図形と周辺の２つ貼り合せて１個分となる図形に分けて数えると，着色部分は６の単位が三角数でふえていくので，合計は，

　　３ｎ（ｎ−１）＋３ｎ＝３ｎ^2

となる．

−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−−

　どんな三角形も４，９，１６，・・・，ｎ^2個に合同分割できることは当然だが，偶数分割点でなく奇数分割点ダイヤグラムの場合も３個単位は変わらないから，３ｎ^2となる．たとえば，３等分してダビデの星を作ってみよう．

　一般に与えられた三角形の各辺を同じ倍率ｋで伸縮した位置に点をとって作った三角形の面積は，もとの三角形の面積の

　　Ｍ＝３ｋ^2−３ｋ＋１＝３（ｋ−１／２）^2＋１／４

倍になるから，

　　ｋ＝１／３　→　Ｍ＝１／３　　（３等分）

　　ｋ＝１／２　→　Ｍ＝１／４　　（４等分）

　　ｋ＝２／３　→　Ｍ＝１／３　　（３等分）

　　ｋ＝１　　　→　Ｍ＝１

　　ｋ＝２　　　→　Ｍ＝７　　　　（７等分）

となる．

　したがって，ダビデの星では互いの辺を３等分し，面積はもとの三角形の面積の４／９に等しい．また，ダビデの星が重なった部分の６角形の面積はもとの三角形の面積の２／９，ダビデの星の面積の１／２に等しい．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝