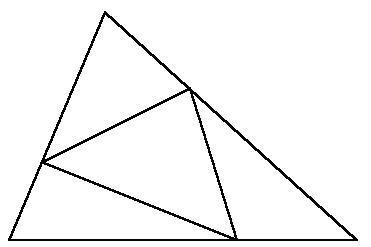
三角形の各辺の３等分点を対頂点と結ぶと，中央部にできる小さな三角形はもとの三角形の７等分になる．それでは，三角形の各辺の３等分点同士を結ぶとどうなるか？　（中川宏）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　任意の三角形の各辺の３等分点を下図のように結ぶと，三角形は３等分される．

　もちろん，もとの三角形の内部にできた小さな４つの三角形は一見していずれも元の三角形と相似ではないし，４つなのに３等分とはどうゆうことかと怪しまれるにちがいない．しかし，４つの三角形を中央，上，左，右の三角形とよぶことにすると，まず，上の三角形の下半分と左の三角形を貼り合わせると，中央の三角形と合同な三角形となる．必要なのは下図に付け加えた平行線である．

　次に，上の三角形の上半分と右の三角形を貼り合わせると，中央の三角形と合同になることを示す．中央の三角形が５つに分解されることになって少し複雑だが，同色の形の対応関係は納得いただけることと思う．

　以上のことを一括して示すと，下図のような色分けとなる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝