今回のコラムでは，中川宏さんによる図形の分割２題を掲げる．とくに「三角形の７等分」はコラム「直角三角形の分割」に掲げた

(1)辺の長さが１：１：√２の直角三角形（４５°，４５°，９０°の三角形，三角定規のひとつ）は同形４つだけでなく，２つの同形にも分割できる特殊な三角形（レプ２三角形）である．

(2)辺の長さが１：√３：２の直角三角形（３０°，６０°，９０°の三角形，三角定規のひとつ）は同形４つだけでなく，３つの同形にも分割できる特殊な三角形（レプ３三角形）である．

(3)辺の長さが１：２：√５の直角三角形は同形４つだけでなく，５つにも分割できる特殊な三角形（レプ５三角形）である．

を受けての話題であると思われる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】三角形の７等分

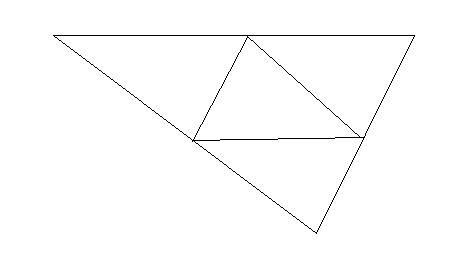
　どんな三角形でも各辺の中点をそれぞれ結んでやれば４等分することができる（一般にどんな三角形も４，９，１６，・・・，ｎ^2個に合同分割できる）．★

　では，三角形の各辺の３等分点のうちの３つを下図のようにとって，もっとも遠い頂点（対頂点）と結ぶとどうなるか（この場合頂点から右側に近い３等分点を選んでいるが，左側に近い点をとることも可能）．

　すると，中央部にできた小さな三角形は，もとの三角形の７等分になる．

　平行線を追加し，中央の三角形（緑色の部分）による平行四辺形の格子を描けば，同色の部分の入れ替えによって周囲に合計６個分の合同な三角形を形成することが理解できるだろう．

［雑感］この方法では一般にもとの三角形とは相似にはならないし，ほかに同形は現れない．（正三角形の場合に相似になるが，それ以外にも相似になることがありそうである）．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】平行四辺形の中線は対角線を３等分する

(1)平行四辺形の２本の対角線はお互いに２等分する．

(2)三角形の重心は中線を２；１に分ける

を使って，以上のことを導くことができる．

［雑感］三角形の７等分は三角形２つ分の図形としての平行四辺形を考えることによっても導かれる（平面幾何の教科書には平行四辺形の関する事柄はほとんどない）．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝