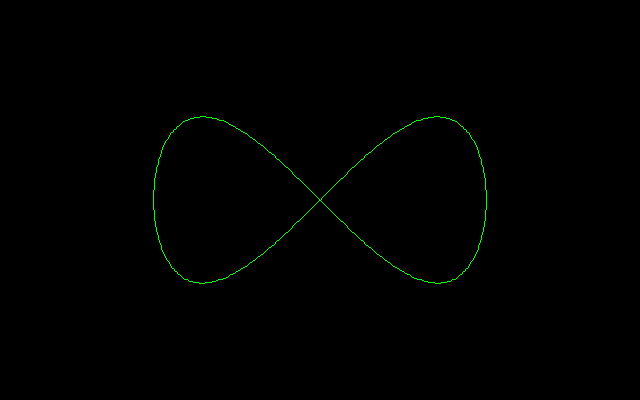
ベルヌーイのレムニスケート：（ｘ^2＋ｙ^2）^2＝（ｘ^2−ｙ^2）は三角関数を用いて

　　ｘ＝ｃｏｓθ／（１＋ｓｉｎ^2θ）＝ｔ（１＋ｔ^2）／（１＋ｔ^4）

　　ｙ＝ｓｉｎθｃｏｓθ／（１＋ｓｉｎ^2θ）＝ｔ（１−ｔ^2）／（１＋ｔ^4）

とパラメトライズされる．ゲロンのレムニスケート：ｙ^2＝ｘ^2−ｘ^4も

　　ｘ＝ｓｉｎθ＝（１−ｔ^2）／（１＋ｔ^2）

　　ｙ＝ｓｉｎθｃｏｓθ＝２ｔ（１−ｔ^2）／（１＋ｔ^2）^2

とパラメトライズされるから，ベルヌーイのレムニスケート：（ｘ^2＋ｙ^2）^2＝（ｘ^2−ｙ^2）もゲロンのレムニスケート：ｙ^2＝ｘ^2−ｘ^4も有理曲線というわけである

　それに対して，フェルマー曲線：ｘ^n＋ｙ^n＝１やｙ^2＝１−ｘ^4は非有理曲線の例である．ベルヌーイのレムニスケートは数学史上重要な意義を果たした曲線であるが，ゲロンのレムニスケートはどうだったのだろうか？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【１】ゲロンのレムニスケートの弧長・周長

　ベルヌーイのレムニスケートは直交座標系では（ｘ^2＋ｙ^2）^2＝（ｘ^2−ｙ^2），極座標系ではｒ^2＝ｃｏｓ２θにより与えられる．したがって，弧長ｓは

　　ｓ＝∫(0,r)（ｄｒ^2＋ｒ^2ｄθ^2）^1/2ｄｒ＝∫(0,r)ｄｒ／√（１−ｒ^4）

すなわち，

　　ｄｓ＝ｄｘ／（１−ｘ^4）^1/2

において，第１種楕円積分∫ｄｓがレムニスケートの求長問題である．

　一方，ゲロンのレムニスケート：ｙ^2＝ｘ^2−ｘ^4の（極座標表示でなく）媒介変数表示

　　ｘ＝ｓｉｎθ＝（１−ｔ^2）／（１＋ｔ^2）

　　ｙ＝ｓｉｎθｃｏｓθ＝２ｔ（１−ｔ^2）／（１＋ｔ^2）^2

を採用すれば

　　ｄｘ／ｄθ＝ｃｏｓθ

　　ｄｙ／ｄθ＝２ｃｏｓ^2θ−１

　　ｓ＝∫(0,θ)（ｄｘ^2＋ｄｙ^2）^1/2ｄθ＝∫(0,θ)√（１＋４ｃｏｓ^2θ）ｓｉｎθｄθ

　変数変換ｚ＝ｃｏｓθを行えば

　　ｄｘ＝ｓｉｎθｄθ

　　ｓ＝∫(1,ａｒｃｃｏｓｚ)√（１＋４ｚ^2）ｄｚ

楕円積分は得られず，

　　ｓ＝１／４［２ｚ√（１＋４ｚ^2）＋ｌｏｇ（２ｚ＋√（１＋４ｚ^2）］(1,ａｒｃｃｏｓｚ)

になる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

【２】ｙ^2＝１−ｘ^4の場合

　ついでに，ｙ^2＝１−ｘ^4の場合を調べてみよう．ｙ^2＝１−ｘ^4はテレビのブラウン管のような押しつぶされた円形になるが，非有理曲線であるから（媒介変数表示でなく）直接直交座標系での方程式を微分すると

　　２ｙｄｙ／ｄｘ＝−４ｘ^3

　　ｄｙ／ｄｘ＝−２ｘ^3／（１−ｘ^4）^1/2

　　ｓ＝∫(0,x)（１＋（ｄｙ／ｄｘ）^2）^1/2ｄｘ

　　　＝∫(0,x)√（１−ｘ^4＋４ｘ^6）／（１−ｘ^4）ｄｘ

厳めしい楕円積分となる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝