以前にアップロードした「楕円積分の加法定理」シリーズは,本コラムのなかでも進んだ考察の部類の記事であると自負しているのだが,今回のコラムではそのエッセンスを抽出して再掲したい.
===================================
【1】円積分の倍角公式
円の4分の1周の長さを求めるのに,y=(1-x^2)^(1/2)に対し,
∫(0,1)(1+(dy/dx)^2)^(1/2)dx
を計算すると,これは
∫(0,1)1/(1-x^2)^(1/2)dx
となります.そこで
f(x)=1/(1-x^2)^(1/2)
2∫(0,1)f(x)dx=3.141592・・・=π
となり,これをπの定義とし,完全円積分と呼ぶことにします.
F(z)=∫(0,z)f(x)dxは不完全円積分ですが,これから円関数(三角関数)を
sinω=F^(-1)(ω),cosω=F^(-1)(π/2-ω)
と定義すると,逆正弦関数
sin^(-1)x=∫(0,x)f(t)dt=u
が得られます.
2u=2∫(0,x)f(t)dt
ですが,三角関数の倍角の公式(あるいは加法定理)
sin2u=2sinucosu=2sinu(1-sin^2u)^1/2=2x(1-x^2)^1/2
より,
2u=sin^(-1)(2x(1-x^2)^1/2)
したがって,
2∫(0,x)f(t)dt=∫(0,2x(1-x^2)^1/2)f(t)dt
2G(x)=G(2x(1−x^2)^1/2)
が成り立ちます.
2x(1-x^2)^1/2はxから四則演算および平方根により得られますので,この式は定規とコンパスだけで円弧長を2倍にする作図が可能であることを示しています.
sinu=x,sinv=y,sin(u+v)=zとおけば,正弦関数の加法公式は
z=x(1−y^2)^1/2+y(1−x^2)^1/2
と表されます.
===================================
【2】レムニスケート積分の倍角公式
ベルヌーイはレムニスケートの弧長を
f(x)=1/(1-x^4)^(1/2)
u=F(x)=∫(0,x)f(t)dt
と表しました.これがレムニスケート積分と呼ばれる典型的な楕円積分です.また,
∫(0,1)f(t)dt=1.311028・・・=ω
とおくと,4ωがレムニスケートの全長になります.円に類比すると,レムニスケートの定数(レムニスケート周率)ωは円に対する円周率πと同じ役割を演じていることになります.
F(x)の逆関数であるレムニスケートサインsl(u)も周期4ωをもつことがわかります.レムニスケートサインを求めてみることにしましょう.実際に1/(1-x^4)^(1/2)を2項展開し,さらに項別積分すると
F(x)=x+1/10x^5+1/24x^9+5/208x^16+・・・
この逆関数のべき級数展開は
sl(u)=u-1/10u^5+1/120u^9+11/15600u^13+・・・
=u(1-1/10u^4+1/120u^8+・・・)
=ug(u^4)
となります.
円積分では
x=sinu,f'(u)=dx/du=1/du/dx=(1-x^2)^1/2=y(=cosu=sin'u)
よりx,yはともにパラメータuの関数になりましたが,レムニスケート積分でもx=sl(u),y=sl'(u)はともにパラメータuの関数になり,曲線y^2=1−x^4はx=sl(u),y=sl'(u)によってパラメータ表示できます.
ここで,sl(2u)をsl(u)の関数として表せればよいことになるのですが,レムニスケートサインの倍角の公式(あるいは加法定理)は
sl(u+v)=(sl(u)sl'(v)+sl(v)sl'(u))/(1+sl^2(u)sl^2(v))
sl(2u)=2sl(u)sl'(u)/(1+sl^4(u))
sl'(u)=(1-sl^4(u))^1/2
sl(2u)=2sl(u)(1-sl^4(u))^1/2/(1+sl^4(u))=2x(1-x^4)^1/2/(1+x^4)
のようになります.レムニスケートサインとその導関数が正弦関数とその導関数である余弦関数にいかに類似しているかわかるでしょう.
2u=sl^(-1)(2x(1-x^2)^1/2/(1+x^4))
したがって,レムニスケート積分の倍角公式
2∫(0,x)f(t)dt=∫(0,2x(1-x^4)^1/2/(1+x^4))f(t)dt
2G(x)=G(2x(1−x^4)^1/2/(1+x^4))
が成り立ちます.
2x(1-x^4)^1/2/(1+x^4)もxから四則演算および平方根により得られますので,円同様,レムニスケートも定規とコンパスだけで弧長を2倍にする作図が可能であることを示しています.
1751年,オイラーは正弦関数の加法定理
G(x)+G(y)=G(x(1−y^2)^1/2+y(1−x^2)^1/2)
との類似に基づいて,レムニスケート積分に対する加法定理
G(x)+G(y)=G((x(1−y^4)^1/2+y(1−x^4)^1/2))/(1+x^2y^2))
を構成することに成功しています.すなわち,
slu=x,slv=y,sl(u+v)=zとおけば,レムニスケート正弦関数の加法公式は
z=(x(1−y^4)^1/2+y(1−x^4)^1/2))/(1+x^2y^2)
あるいは,同じことですが
z=(x(1−y^4)^1/2+y(1−x^4)^1/2))/(1+x^2y^2)
のとき,
f(x)=1/(1-x^4)^(1/2)
∫(0,z)f(t)dt=∫(0,x)f(t)dt+∫(0,y)f(t)dt
と表されます.
===================================
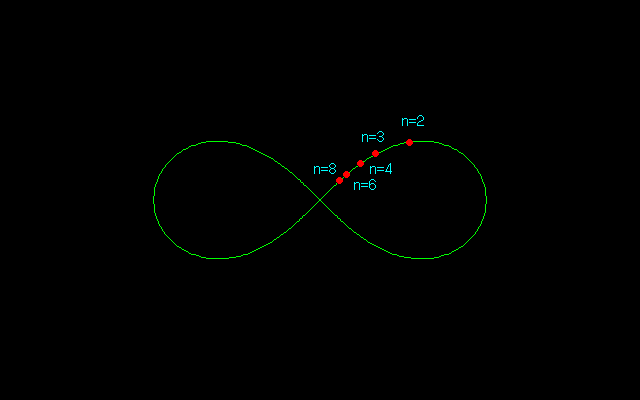
【3】ベルヌーイのレムニスケートのn等分点
ベルヌーイのレムニスケートの方程式は
(x^2+y^2)^2=x^2−y^2
である.
第1象限にある部分だけを考えることにして,この弧は原点O(0,0)を始点,P(1,0)を終点としてパラメータz(0≦z≦1)を用いれば,
x^2=1/2(z^2+z^4),y^2=1/2(z^2−z^4)
と表せる.
この線素は
ds=(dx^2+dy^2)^1/2=dz/(1−z^4)^1/2
で与えられ,倍角公式
z→2z(1−z^4)^1/2/(1+z^4)
はdsを2dsに変える.
2z(1−z^4)^1/2/(1+z^4)=1
と置くことによって
z^2=√2−1
が得られる.以上より,
z (x,y)
n=2 → 0.643594 → (0.541196,0.348311)
n=3 → 0.435421 → (0.335810,0.277170)
n=4 → 0.327379 → (0.243582,0.218735)
n=6 → 0.218456 → (0.158115,0.150741)
n=8 → 0.163865 → (0.117415,0.114304)

===================================
【4】反転公式
写像
z→{(1−z^2)/(1+z^2)}^1/2
によりOとPは移り合い,弧OPは自分自身に移り弧長OPは保存される.
Qを弧OP上の点とするとき,弧OQは等しい長さの弧QPに移される.したがって,
z (x,y)
n=2 → 0.643594 → (0.541196,0.348311)
n=3 → 0.435421 → (0.335810,0.277170)
n=4 → 0.327379 → (0.243582,0.218735)
n=6 → 0.218456 → (0.158115,0.150741)
n=8 → 0.163865 → (0.117415,0.114304)
は,
z (x,y)
n=2 → 0.643594 → (0.541196,0.348311)
n=3 → 0.825378 → (0.756753,0.329506)
n=4 → 0.897995 → (0.853426,0.279394)
n=6 → 0.953363 → (0.931398,0.203496)
n=8 → 0.973499 → (0.960687,0.157423)
に移る.
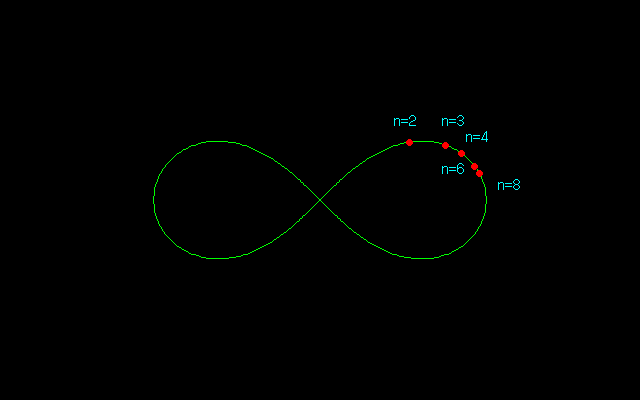
レムニスケート積分に対する加法定理
G(x)+G(y)=G((x(1−y^4)^1/2+y(1−x^4)^1/2))/(1+x^2y^2))
において,とくに,y=1の場合,反転公式
z→{(1−z^2)/(1+z^2)}^1/2
y=xの場合,倍角公式
z→2z(1−z^4)^1/2/(1+z^4)
を与えるというわけである.
===================================
【5】レムニスケート関数と三角関数の類似性
レムニスケート関数と三角関数の類似性がレムニスケート関数の理論を構築する助けとなった.
[1]円の場合
円:x^2+y^2=1→x+ydy/dx=0
の線素は
ds=(dx^2+dy^2)^1/2=dx/(1−x^2)^1/2
で与えられる.
倍角公式
x→2x(1−x^2)^1/2
はdsを2dsに変える.
また,反転公式
x→(1−x^2)^1/2
によりO(0,0)とP(1,0)は移り合い,弧OPは自分自身に移り弧長OPは保存される.
y^2=F(x)=1−x^2
とおくと,
ds=dx/y=dx/(1−x^2)^1/2
このとき,微分方程式
dx/(1−x^2)^1/2=dy/(1−y^2)^1/2
の一般解は
x^2+y^2=c^2+2xy(1−c^2)^1/2
で与えられる.
c=0の場合が自明な解x=y,c=1の場合が反転公式
y=(1−x^2)^1/2
である.
一般解はyに関する2次方程式
y^2−2yx(1−c^2)^1/2+x^2−c^2=0
を解いて,
y=x(1−c^2)^1/2±c(1−x^2)^1/2
ここで,適宜変数を置き換えると,加法・減法公式
z=x(1−y^2)^1/2±y(1−x^2)^1/2
が得られる.
[2]レムニスケートの場合
ベルヌーイのレムニスケートの方程式は
(x^2+y^2)^2=x^2−y^2
である.第1象限にある部分だけを考えることにして,この弧は原点O(0,0)を始点,P(1,0)を終点としてパラメータz(0≦z≦1)を用いれば,
x^2=1/2(z^2+z^4),y^2=1/2(z^2−z^4)
と表せる.(x,y)を楕円関数でパラメトライズしたというわけである.
この線素は
ds=(dx^2+dy^2)^1/2=dz/(1−z^4)^1/2
で与えられ,倍角公式
z→2z(1−z^4)^1/2/(1+z^4)
はdsを2dsに変える.
したがって,レムニスケートの2等分点を求める際,
sl(2z)=2z(1−z^4)^1/2/(1+z^4)=1
とおいてzを求めたあと,
x^2=1/2(z^2+z^4),y^2=1/2(z^2−z^4)
により,2等分点(x,y)を求めなければならないことになる.
また,反転公式は
z→{(1−z^2)/(1+z^2)}^1/2
で与えられる.
y^2=F(x)=1−x^4
とおくと,
ds=dx/y=dx/(1−x^4)^1/2.このとき,微分方程式
dx/(1−x^4)^1/2=dy/(1−y^4)^1/2
の一般解は
c^2x^2y^2+x^2+y^2=c^2+2xy(1−c^4)^1/2
で与えられる.
c=0の場合が自明な解x=y.c=1の場合,すなわち,
x^2y^2+x^2+y^2−1=0
y^2=(1−x^2)/(1+x^2)
が反転公式である.
一般解はyに関する2次方程式
y^2(1+c^2x^2)−2yx(1−c^4)^1/2x+x^2−c^2=0
を解いて,
y={x(1−c^4)^1/2±c(1−x^4)^1/2}/(1+c^2x^2)
ここで,適宜変数を置き換えると,加法・減法公式
z={x(1−y^4)^1/2±y(1−x^4)^1/2}/(1+x^2y^2)
が得られる.
===================================
【6】レムニスケートのパラメータ表示
原点を中心とする半径1の円の円周上の点を(x,y)とすれば,第3の変数θを媒介として,x=cosθ,y=sinθと表されます.θは(x,y)と(0,0),θ/2は(x,y)と(−1,0)を結ぶ直線とx軸とのなす角を表しています.
さらにt=tan(θ/2)とすると
tan(θ/2)=sinθ/(1+cosθ),
cosθ=(1−t^2)/(1+t^2),
sinθ=2t/(1+t^2)より,
x=±(1−t^2)/(1+t^2),
y=2t/(1+t^2) (−1≦t≦1)
と表すことができます.
また,a=1/√2のとき,レムニスケート:r^2 =cos2θ,(x^2 +y^2 )^2 =x^2 −y^2 は,
x=cosθ/(1+sin^2θ)
y=sinθcosθ/(1+sin^2θ)
ここで,
sinθ=(1−t^2)/(1+t^2)
cosθ=2t/(1+t^2)
とおくと,
x=t(1+t^2)/(1+t^4 )
y=t(1−t^2)/(1+t^4 )
のようにパラメトライズすることができます.
===================================
【7】ゲロンのレムニスケート
レムニスケートといえば,一般にベルヌーイのレムニスケートを指す場合が多いが,もともと8の字曲線を表す用語であり,Geronoのレムニスケート,Boothのレムニスケート,Montferrierのレムニスケート,Slueseのレムニスケートなど多くのレムニスケートがあるそうだ.Geronoのレムニスケート:(x,y)=(cosθ,sinθcosθ)はリサージュ曲線の1つとして知られている.
コラム「楕円積分の加法定理(その8)」において,『ベルヌーイのレムニスケートは三角関数を用いて
x=cosθ/(1+sin^2θ)
y=sinθcosθ/(1+sin^2θ)
とパラメトライズされるが,阪本氏によるとGegoroのレムニスケート
x=sinθ
y=sinθcosθ
というのもあるそうだ.以下にGegoroの連珠形を掲げる.
』と記したが,阪本氏が
[参]グレイ「曲線と曲面の微分幾何」小島順監訳,竹沢護訳,トッパンを参考にした際にスペルミスしたもので,Geronoが正しい.ゲロンはフランスの数学者.
ベルヌーイのレムニスケート:(x^2+y^2)^2=(x^2−y^2)は三角関数を用いて
x=cosθ/(1+sin^2θ)=t(1+t^2)/(1+t^4)
y=sinθcosθ/(1+sin^2θ)=t(1−t^2)/(1+t^4)
とパラメトライズされる.ゲロンのレムニスケート:y^2=x^2−x^4も
x=sinθ=(1−t^2)/(1+t^2)
y=sinθcosθ=2t(1−t^2)/(1+t^2)^2
とパラメトライズされるから,ベルヌーイのレムニスケート:(x^2+y^2)^2=(x^2−y^2)もゲロンのレムニスケート:y^2=x^2−x^4も有理曲線というわけである
それに対して,フェルマー曲線:x^n+y^n=1やy^2=1−x^4は非有理曲線の例である.ベルヌーイのレムニスケートは数学史上重要な意義を果たした曲線であるが,ゲロンのレムニスケートはどうだったのだろうか?
===================================