フェルマーらせん(r2=aθ)と黄金角が結びつくと、原点付近から無限遠まで一様な点分布が形成される.

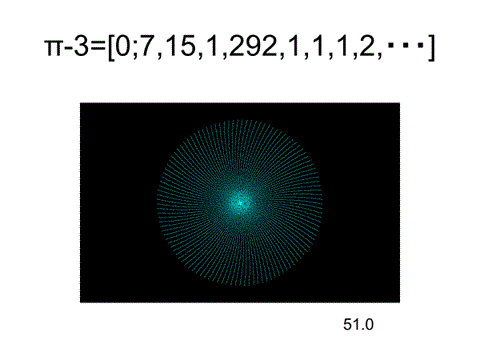
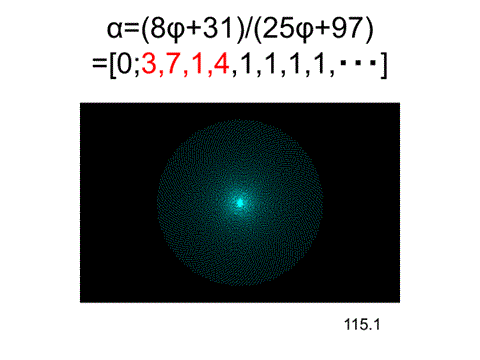
らせんの形状と開度αを変化させて無限遠での振る舞いを調べる。植物の話ではないのであるが、無限に大きいヒマワリを仮想する. それが無限遠で一様分布になるためにはフェルマーらせんで、αの連分数展開の部分商が有限に限ることが証明されている.

次に、アルキメデスらせんの例を掲げるが、いずれも無限遠で一様分布にならないことを示す。パッと見分けるのは難しいこともあるが・・・

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

360×(√5-1)/2=222.5°

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

360×(π-3)=51.0°

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

360×(8φ+31)/(25φ+97)=115.1°

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

360×(31φ+157)/(46φ+233)=246.3°

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝