正五角形の1辺と対角線の長さの比が1:φであることを知ったのは中学生の頃だっただろうか。

先生が示したものは補助線を引いて証明するものであったのだが、その後、自ら補助線を引かない証明法を思いついたことを覚えている。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

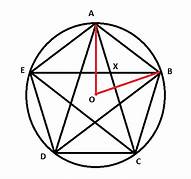
AB=1,AX=BX=xとおく。

対角線はx:1-x:xに分割される。対角線の長さは1+xとなる。

中央の二等辺三角形に注目すると相似比

x:1-x=1+x:1

x=1-x^2

x^2+x-1=0→x=(-1+√5)/2

対角線の長さは1+x= (1+√5)/2

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝