［１］回転する正三角形の追跡問題

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

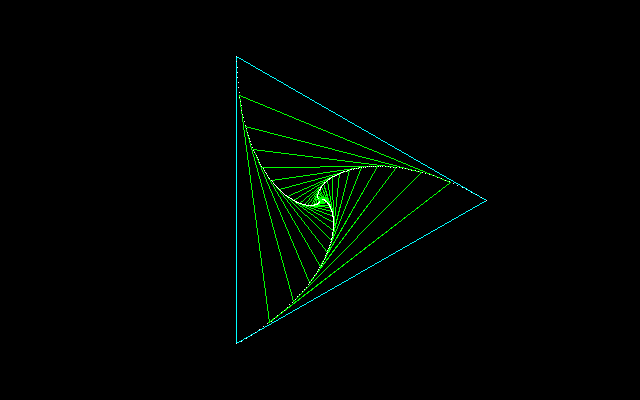
　３匹のアリが正３角形の頂点に１匹ずついたとして，それぞれ同じ速さで隣りのアリを追いかけるとする．この場合は，アリのたどる軌跡は等角らせんを描いて、正三角形の中心に収束していく。

　３匹のアリが一直線上にいる、あるいは、正三角形ではない三角形になっている場合も含め、速さ1で動く運動方程式を考えると

-da/dt=1+cosC

-db/dt=1+cosA

-dc/dt=1+cosB

ここで、余弦定理：c^2=a^2+b^2-2abcosCを用いると

-da/dt=1+(a^2+b^2-c^2)/2ab=(a+b+c)(a+b-c)/2ab

-db/dt=1+(b^2+c^2-a^2)/2bc=(a+b+c)(-a+b+c)/2bc

-dc/dt=1+(c^2+a^2-b^2)/2ca=(a+b+c)(a-b+c)/2ca

2abc/(a+b+c)をかけ、新しいパラメータ

x=b+c-a

y=c+a-b

z=a+b-cを導入すると

-dx/dt=xy,-dy/dt=yz,-dz/dt=za

と簡単な形になる

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

３匹のアリの位置関係を正三角形の各辺からの距離がx,y,zに比例するように選ぶと、それぞれの位置関係が作る三角形は合同か相似になる。 x/y+y/z+z/xは絶えず増加している。３匹のアリの作る三角形は扁平になっていき、直線に近づく。扁平になった三角形にアリの運動はらせんのような運動になり、３匹のアリは順番に真ん中の位置になる

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝