2次元ハニカム構造は6角形、3次元ハニカム構造は14面体によってつくられる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

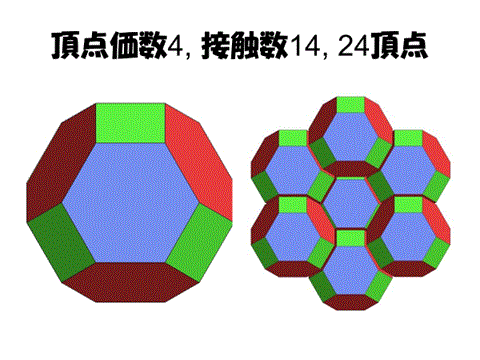
安定な構造をどう考えるかを拡張させる方向としては、一つには次元を上げることが考えられる。

c2=6→c3=14→c4=?

実はこの解は(cn)=(cn-1)+2^n, c1=2で与えられる。4次元ハニカム構造は30胞体によってつくられるというわけである。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

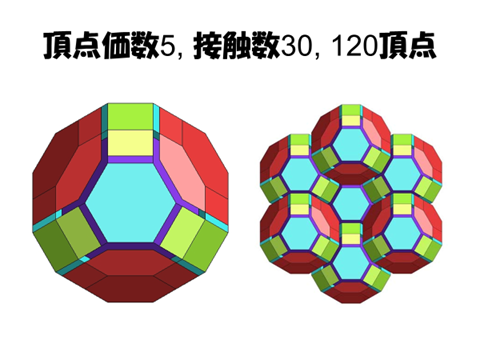
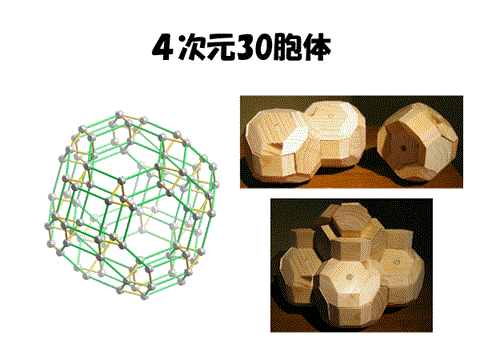
この漸化式が解ければ、Cn=2(2^n-1) となり、ｎ次元のハニカム構造は

[1]頂点価数n+1 (ルベーグの舗石定理)

[2]接触数2(2^n-1) (ミンコフスキーの舗石定理)

[3]頂点数は(n+1)!

すなわち,置換多面体=原始的平行多面体となることがわかるだろう。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
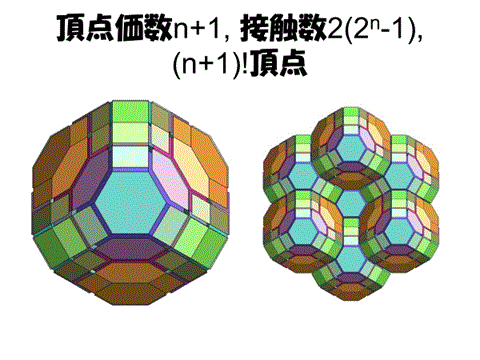