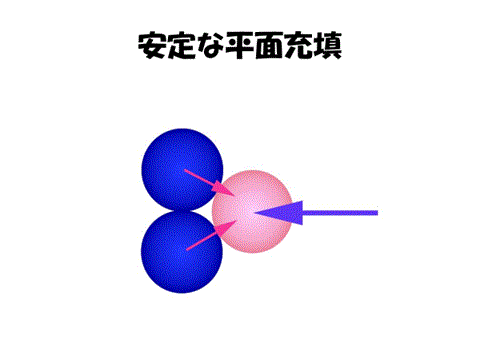
つまるところ、安定な平面充填とは2個の細胞で1個の細胞の動きをフレキシブルに受け止められる構造（すなわち頂点価数3）である。3次元では3個の細胞で1個の細胞の動きをフレキシブルに受け止められる構造（すなわち頂点価数4）であると考えることができるだろう。(=3次元の平衡分割）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

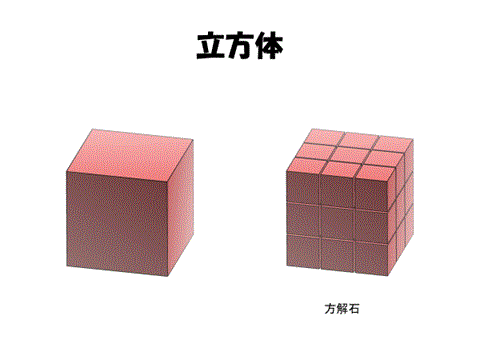
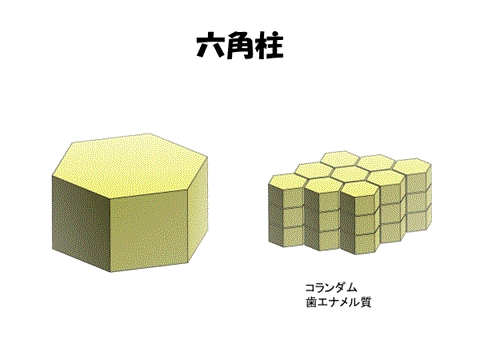
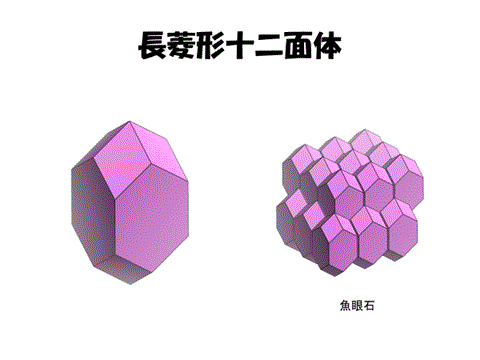
そのような形は何面体になるのか？　その候補を5つの平行多面体に限定して考えてみよう。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

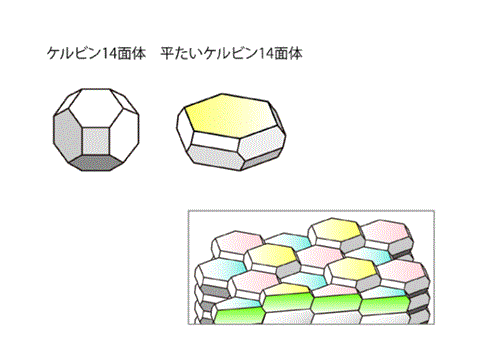
これらの中で頂点価数4であるのは切頂八面体（ケルビンの14面体）だけである。

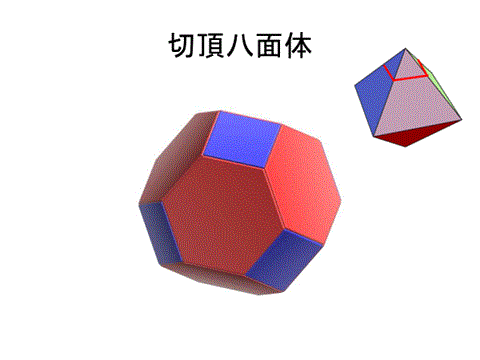
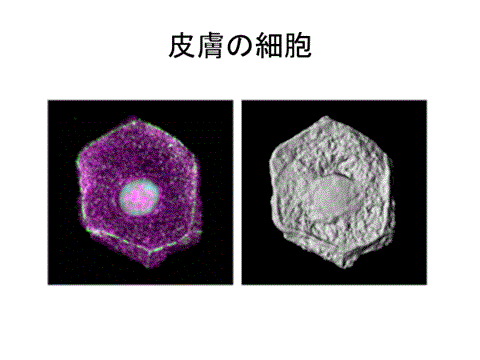
表皮細胞は扁平な形をしているが、14面体による空間充填の1例である。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

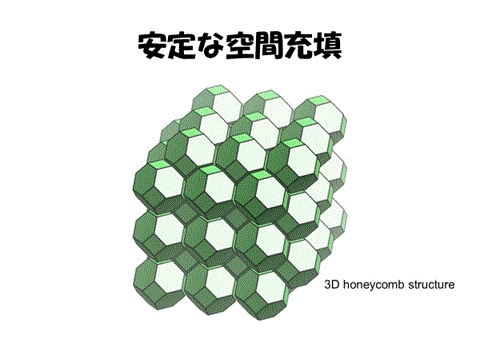
切頂八面体による空間充填は安定であり、それは3次元のハニカム構造と考えられるのである。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
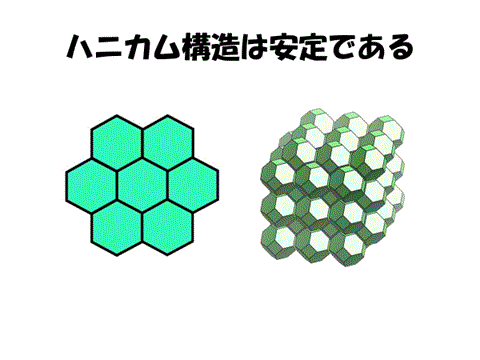