平面図形では分解合同定理が成り立つ。

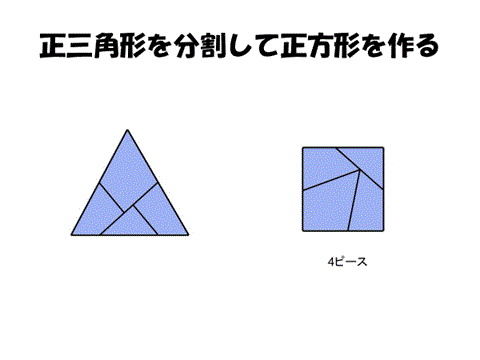
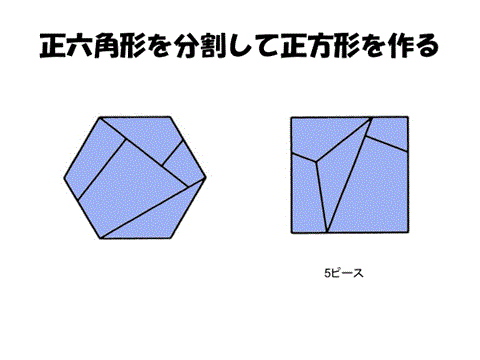
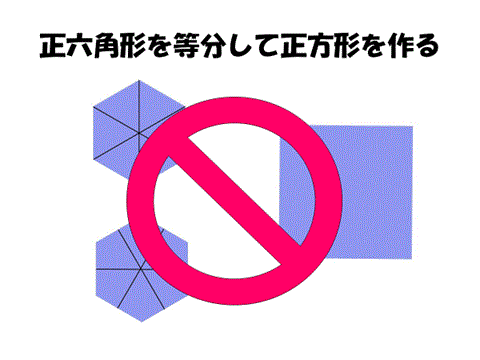
しかしながら、正三角形を等分したピースを組み合わせて、正方形を作ることは不可能だろう。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

空間図形では等分・非等分に関わらず分解合同定理が成り立つことは例外的であり、正四面体を立方体に変身させることは不可能である。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

ところが５種類ある平行多面体はいずれもデーン不変量が0であり、相互に変身させることは可能である

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

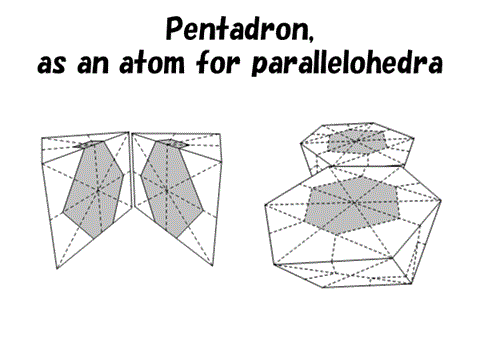
それでは、ある平行多面体を等分した1種類のピース(対称なピースは1種類とみなすことにする） から、ほかの平行多面体を作ることは可能だろうか？

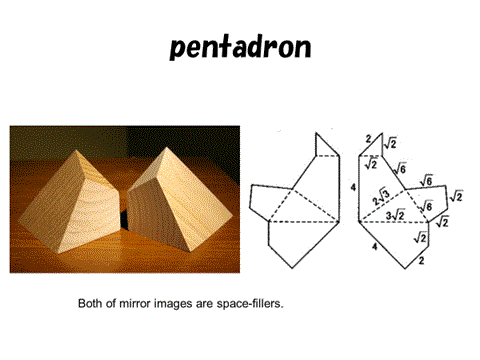
これに対しては懐疑的な意見が多かったのであるが、空間図形は一筋縄ではいかない。実は平行多面体ではこれが可能であって、この図形は秋山仁先生によりペンタドロンと名付けられている。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝