正単体はKn+1完全グラフの形に投影することができる。その場合、中心部は拡大され、周辺部は圧縮される。

この関係はエッシャーの描いた「天国と地獄」を想起させる。そこでは白い天使と黒い悪魔が円板を埋め尽くしている。

その意味で、ポアンカレの双曲円板の正単体版ともいえる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

ユークリッド平面内の双曲平面のモデルとしては

[1]ベルトラミ・クラインモデル(BK)

[2]ポアンカレモデル(P)

[3]上半面モデル(H)

があるが、[1][2]はそれ自身の境界をもたない一つの円である。

前者では直線はユークリッド的線分であるが、角は違った方法で測らなければならない。

後者では角はユークリッド的であるが、直線は円周に垂直な円弧である。

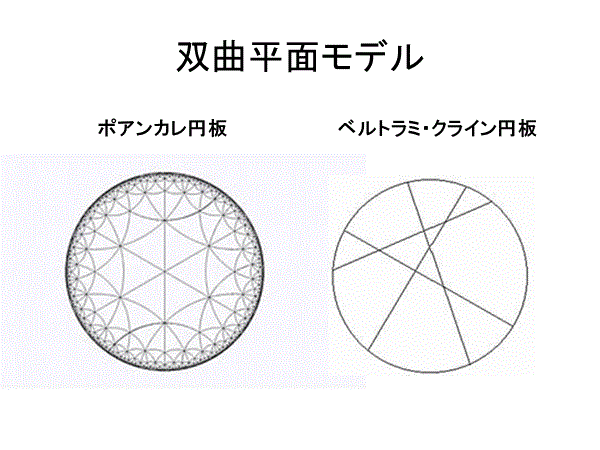
ポアンカレの双曲円板の正単体版よりも,クラインの双曲円板の正単体版といったほうがいいかもしれない。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

ポアンカレ円板がエッシャーの芸術作品に利用されたのに対して、,クラインの双曲円板が芸術に利用された例を知りません。 しいていえば、ピザ分割問題でしょうか？

【Q】１つの円をｎ本の弦で分割する．その際，分割によってできる領域が最も多くなるようにする．最大分割領域数Ｓnはいくつになるか？

（答）この問題は実は円という条件を取り去っても同じ答えになります．すなわち，平面をｎ本の線で分割する．その際，分割によってできる領域が最も多くなるようにする．最大分割領域数Ｓnはいくつになるか？

　分割される領域数が最大になるためには，新しい線（弦）を引くとき，それ以前のすべての線（弦）と新しい交点で交わるようにします．既存の交点を通ると分割される領域が最大数にならないからです．

　　Ｓ0＝１，Ｓ1＝２，Ｓ2＝４，Ｓ3＝７

はすぐに求められます．このことからｎ本目の線（弦）を引くと新しい領域がｎ個増えることがわかります．これを式で表すと

　　Ｓn＝Ｓn-1＋ｎ

　　Ｓn＝Ｓn-1＋ｎ

　　Ｓn-1＝Ｓn-2＋ｎ−１

　　・・・・・・・・・・

　　Ｓ1＝Ｓ0＋１

　　Ｓ0＝１

を辺々加えると，一般式

　　Ｓn＝１＋（１＋２＋３＋・・・＋ｎ）＝１＋ｎ（ｎ＋１）／２

　　　 ＝（ｎ^2＋ｎ＋２）／２

が得られます．

　　Ｓ0＝１，Ｓ1＝２，Ｓ2＝４，Ｓ3＝７，

　　Ｓ4＝１１，Ｓ5＝１６，Ｓ6＝２２，・・・

と続くというわけです．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝