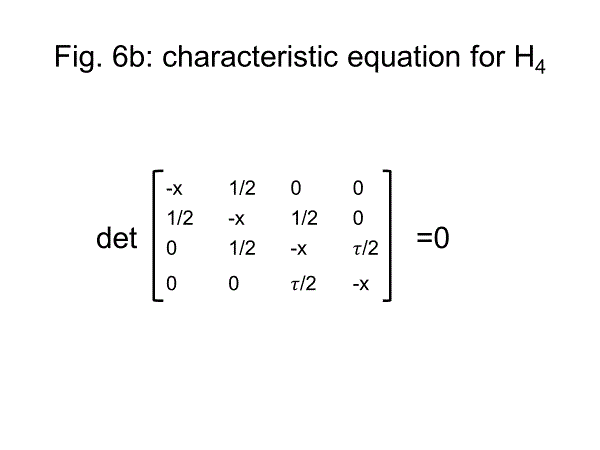���C�[�^�����e�[�^���i���̂R�Q�j
���m�h���~�[�ϊ��̓�����������
��=��(��-exp(2��imi/h)
�ŗ^������B����͉~���������Ȃ̂ň������������B
h=�R�N�Z�^�[��
�R�N�Z�^�[�ϊ��̌ŗL�l��exp(2��imi/h)�Ƃ��āA0��m1��m2���E�E�E��ml�����ƒu�����Ƃ��A�������x�L�w���ƌĂԂ��A
degPi=mi+1
�Ȃ�W�������藧�B
����������������������������������������������������������������������
a) A3=[3,3]
The truncated octahedron is the primitive of A3 (also non-primitive of B3) and the characteristic equation results in the second kind of Chebyshev polynomial;
U3(x)=8x3-4x=0, m={mi}={1,2,3}.
��mi=1+2+3=6 (Antipodal distance of primitive n-parallelotope is given as n(n+1)/2.)
��(mi+1)=2�3�4=24 ((n+1)! vertices in primitive n-parallelotope.)
Note that {mi+1}={2,3,4} reveals double, triple and quadruple rotational symmetry and ��2(x) ��3(x) ��4(x) implies factorization of finite discrete space.
����������������������������������������������������������������������
b) B6=[3,3,3,3,4]
The characteristic equation (Fig. 6a) has resulted in the first kind of Chebyshev polynomial.
T6(x)=32x6-48x4+18x2-1=0, m={mi}={1,3,5,7,9,11}. G(x)= ��2(x) ��4(x) ��6(x) ��8(x) ��10(x) ��12(x).
��mi=1+3+5+7+9+11=36 (Antipodal distance is 36 and n2 in bi-submodular n-polytope.)
��(mi+1)=2�4�6�8�10�12=46080 (=2n�n! vertices in bi-submodular n-polytope.)
Note that the number of reflecting hyperplanes and parallel-edge pairs of the primitives are n(n+1)/2 in An and n2 in Bn.

����������������������������������������������������������������������
c) H4=[3,3,5]
The characteristic equation (Fig. 6b) has resulted in linear combination of Chebyshev polynomials.
2��2T4(x)-U4(x)=0, ��=(1+��5)/2, m={mi}={1,11,19,29}. G(x)= ��2(x) ��12(x) ��20(x) ��30(x).
��mi=1+11+19+29=60, antipodal distance is 60.
��(mi+1)=2�12�20�30=14400 vertices.
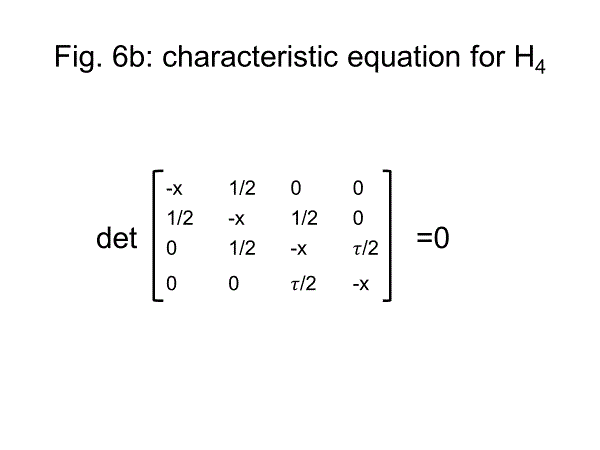
����������������������������������������������������������������������