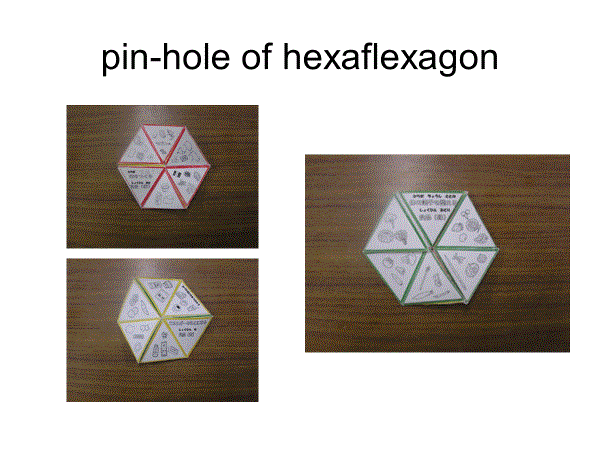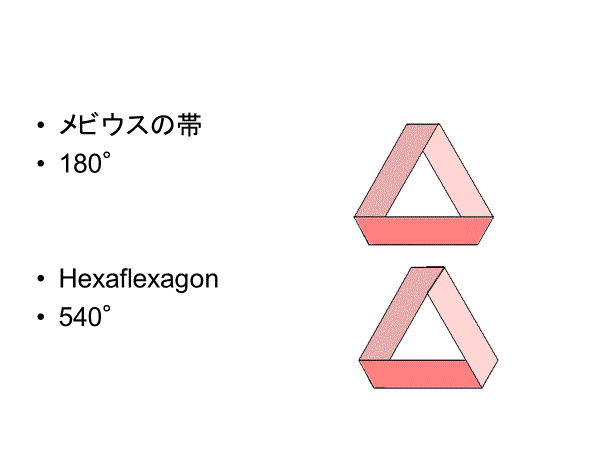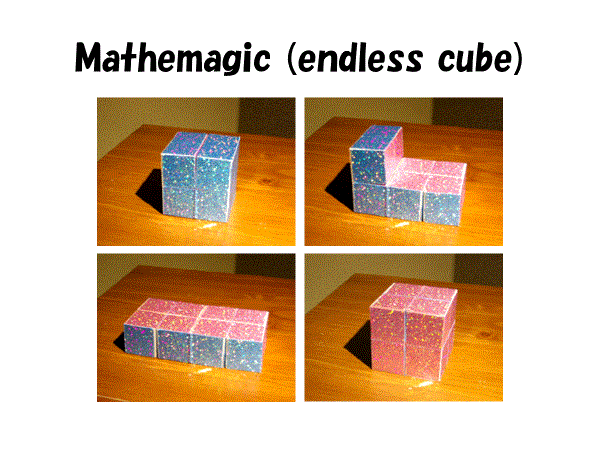エンドレスキューブとは、立方体を２×２×２に８等分する．８個の小立方体を８カ所で繋げる．連結の位置関係は実におもしろく，そのように繋げばバラバラになることなしに，６面×８個＝４８面すべてをみせることができる．たとえば，表面２４個にロンドンの観光写真を載せれば，裏面（隠れている面）２４個にパリの観光写真を載せることができるのである．

ところが、一口に「裏返す」といっても、その内容は多彩である。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

［１］reversion

　パズル作家デュドニーが１９０２年に見つけたとされる．正三角形を正方形に（正方形を正三角形に）する４片裏返しなしの有名なパズルであり，ヒンジで４片を回転させて正三角形と正方形を相互変換させる．デュドニー分割では，正三角形の周は正方形の内部に移り，正方形の周は正三角形の内部の点だけから構成されている．

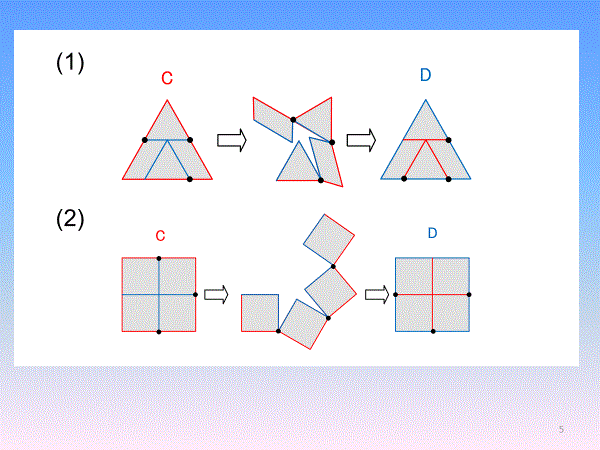
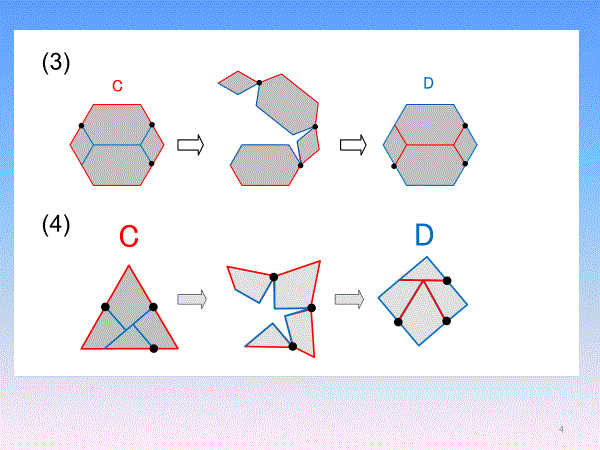
［２］kaleidocycle

連続回転する多面体の環で、パウル・シャッツ・リングやヘキサフレクサゴンがこれに相当する。メビウスの輪は180度のねじれであるが、ヘキサフレクサゴンは540度、パウル・シャッツ・リングも540度のねじれがある。

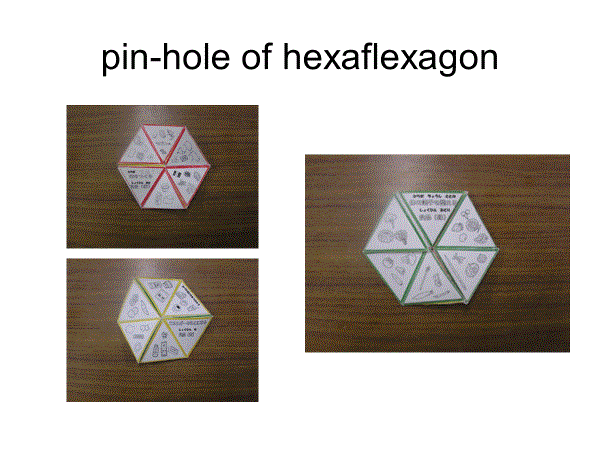
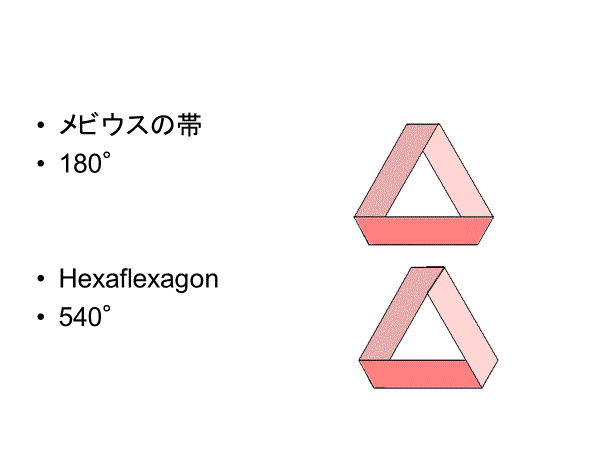
［３］endoless reversion (reversion+kaleidocycle)

適当な稜が蝶番でつながれた８つの立方体の輪も立方体（２×２×２）に折りたたむことができる．表の２４面を裏返すと裏の２４面が現れてくることを利用して観光地の写真を貼り付けてあるおみやげグッズもある．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝
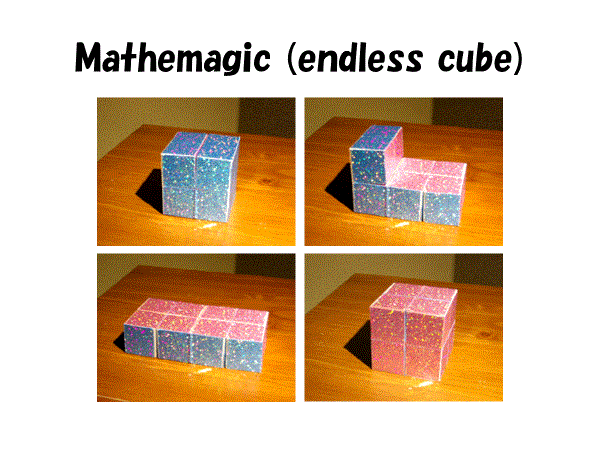