[３]正四面体の連続する３辺をを伸縮させて、２種類の二等辺三角形面からなる四面体の場合

の定義域はそれぞれ、

[３]７２-１４４°

と求まった。

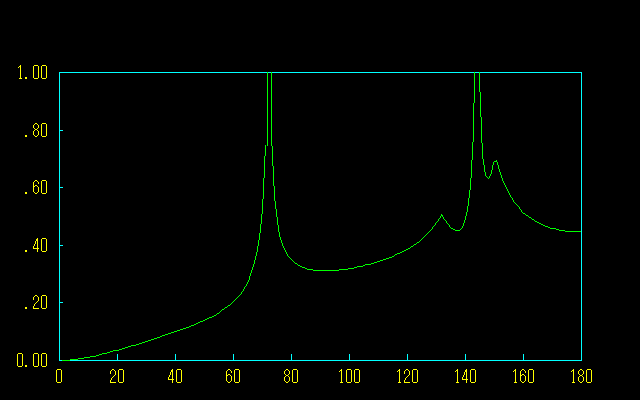
　球の充填率は周期性らせんのみならず、非周期的らせんでも、同じ式で表されることが分かった。

　　ρ＝ｒ^3/ｈ(ｒ+１)^2・4/3

　ｈ→０の場合は発散してしまうことが避けられない。そこで、発散することを気にせず、充填の状態をチェックしてみたい。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

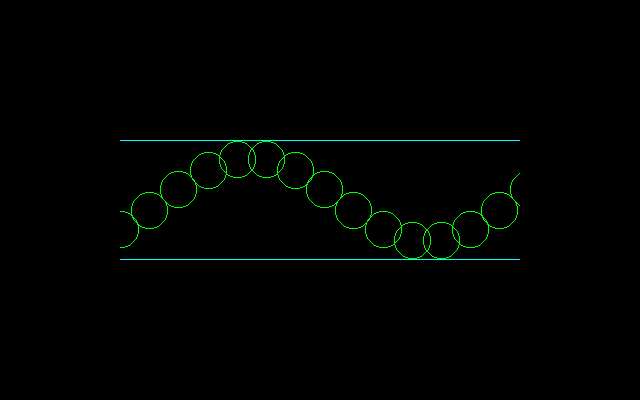
　ねじれ角30°

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

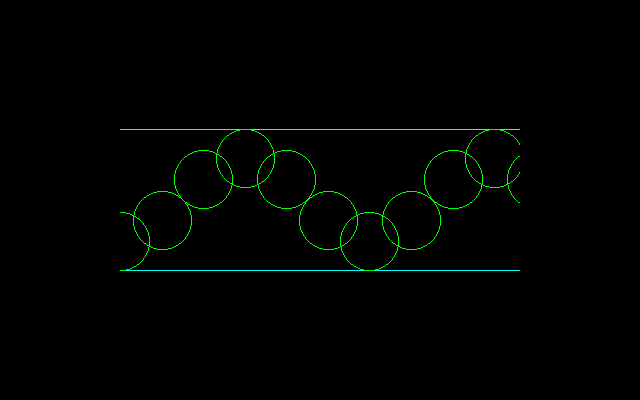
　ねじれ角60°

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

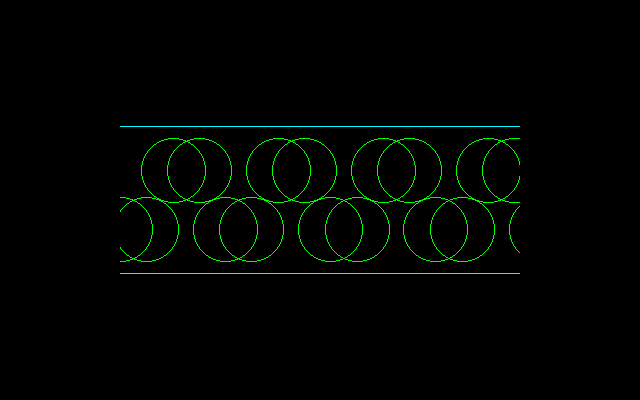
　ねじれ角90°

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　ねじれ角120°

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　ねじれ角150°

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

　ねじれ角180°

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝