■主従逆転型ハイポサイクロイド(その47)
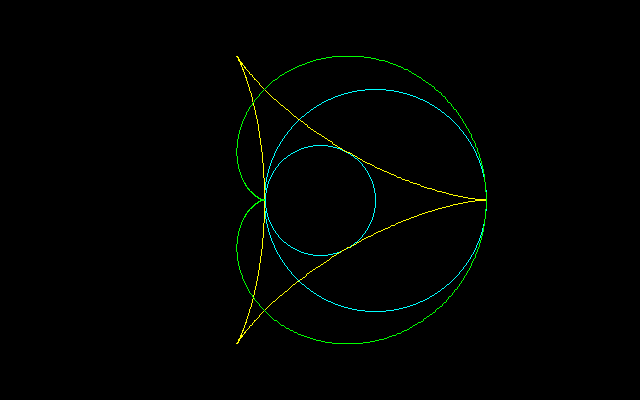
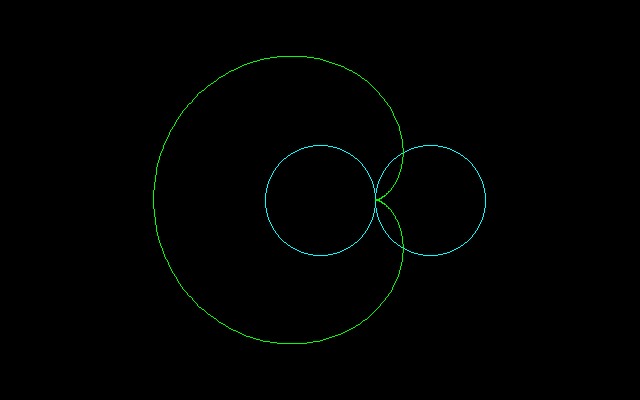
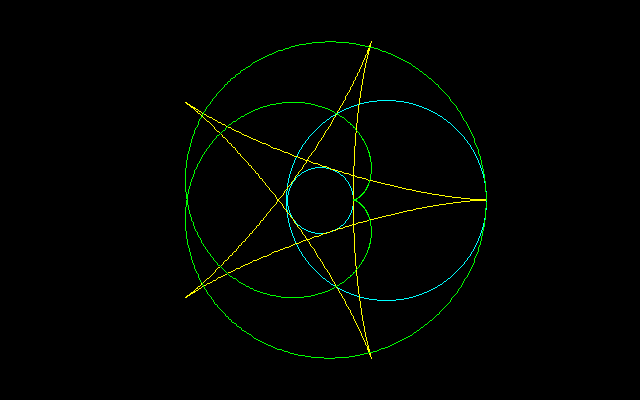
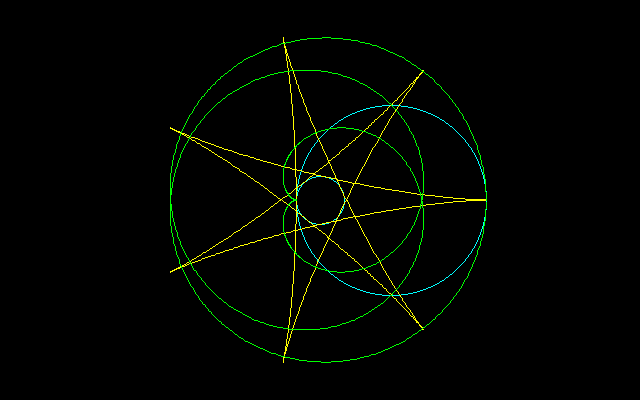
x=(R−r)cosθ+Rcos(+/-(R−r)/Rθ)
y=(R−r)sinθ−Rsin(+/-(R−r)/Rθ)
一般に
x=acosmθ+bcosnθ
y=asinmθ+bsinnθ
で表される曲線をエピサイクリックという。
原点を中心とする半径aの円周上を等速に動く点があり、 その点の周りを半径bで等速に回る点の軌跡である。
デルトイドはハイポサイクロイドやペリトロコイド曲線として描くことができる。
デルトイドで囲まれた図形の中で線分が自分自身の周りに1回転できる。
一般に、線分が自分自身の周りの1回転できるずけいでは、その面積をいくらでも小さくできるという面白い結果が得られている(掛谷・ベシコビッチの問題)
===================================
[1]R=2r
===================================
[2]R=3r

===================================
[3]R=4r

===================================
[4]R=5r
===================================










