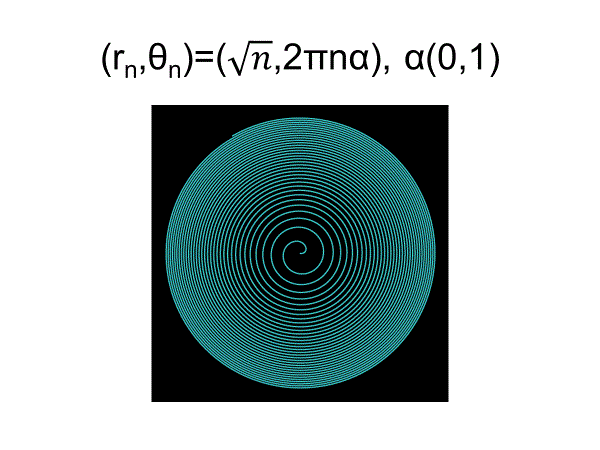ところで、ヒマワリの花序

を問題にするとき、葉序則 (phyllotaxis)として

[1]アルキメデスらせん上の点配置 (r=aθ)?

[2]フェルマーらせん上の点配置 (r^2=aθ)?

の両方が用いられている。これも紛らわしさの原因となっているが、黄金角とは360°を1:τに内分した角度(137.5 / 222.5°)であるが、葉序則は偏角θの規則性であって，動径rの規則ではないことによるものであろう

[3]アルキメデスらせんとフェルマーらせんの中間的ならせん上の点配置 (r^1.5=aθ)? なども考えられると思われるが、ここでは[1]と[2]を比較してみることに会いたい

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

まず、アルキメデスらせん上に点配置 (r=aθ)してみると、中央部ほど密集することが見て取れるだろう。

重ならないようにするにが、中心部を小さく描くことが必要である

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

フェルマーらせん上の点配置 (r^2=aθ)と比較してみる。

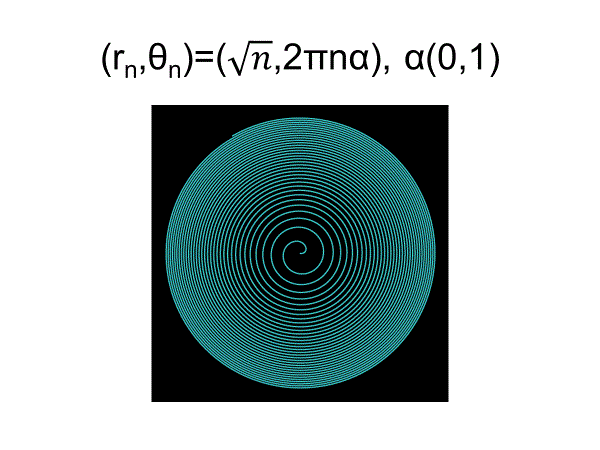
アルキメデスらせん上に点配置とくらべ、 不即不離集合 (Delone set)になっていることがわかる。

すなわち、Voronoi領域の面積がほぼ一定＝点分布の一様性を示している

言い換えれば、これは最も効率の良い配置であって、一様分布になるためにはフェルマーらせんに限ることが証明されている(r^2=aθ, r=aθ^1/2)

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝