【２】ルーローの三角形

　　ｘ（θ）＝２／√３∫(-π/2,θ)（ｓｉｎθ＋（ｓｉｎ^2θ＋２）^1/2）ｄθ

＝−２｛ｃｏｓθ−√２Ｅ（−１／２）−√２Ｅ（θ，−１／２）｝／√３

　　ｙ（θ）＝−２（ｓｉｎθ＋（ｓｉｎ^2θ＋２）^1/2）／√３

　　（-5π/6≦θ≦-π/6）

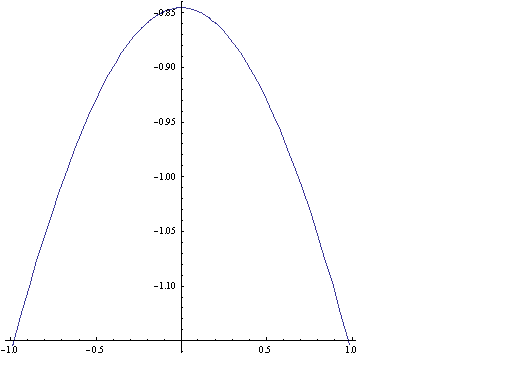
　ルーローの三角形の場合の道の形についてはこの曲線（-5π/6≦θ≦-π/6）が連なった形になります．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝