１８９１年，ロシアの結晶学者フェドロフは平面のあらゆる周期的タイル貼りが１７の対称群のいずれかに属することを証明しました．それでは，非周期的タイル貼りについては何がわかっているのでしょうか？

格子

に対して、非周期的配列を掲げます

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

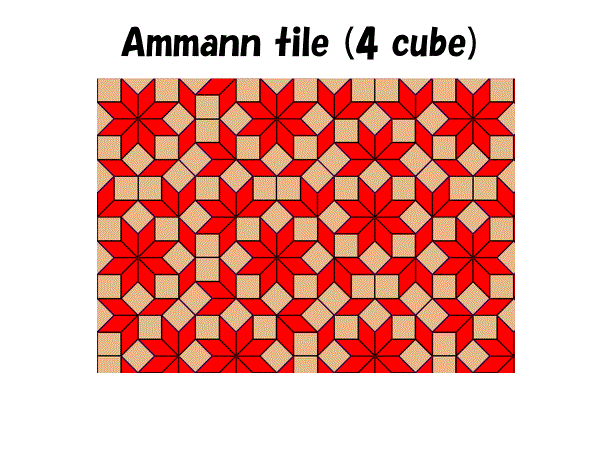
正１０角形を構成する２種類の菱形で構成される準周期性平面充填をペンローズ・パターンというのですが，それに対して，正８角形を構成する２種類の菱形（正方形を含む）で構成される準周期性平面充填はアマン・パターンと呼ばれるタイル貼りになっています．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

１９７４年にイギリスの数理物理学者ペンローズの発見した２種類の菱形を組み合わせて平面を非周期的に敷きつめるものが最も構成要素の少ないものです．２種類の菱形は（ 72°-108°，36°-144°）は正十角形の中心角π／５から導かれたもので、５回回転対称が現れる．P3: 太った菱形（７２°，１０８°）とやせた菱形（３６°，１４４°）２種類の菱形を組み合わせ。最小の内角は３６°であり，他の角はすべてその整数倍で，太めの菱形と細めの菱形の面積比は黄金比φになっています．また，１辺の長さを１とすると太めの菱形の対角線の長さはφ，細めの菱形の対角線の長さは１／φ，さらに，太めの菱形と細めの菱形の個数の比もφとなり，５回対称性のなかには黄金比φが潜んでいます． あとになって，ペンローズ図形が５次元超立方格子の投影図になっていることがド・ブリュインによって示されることになる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

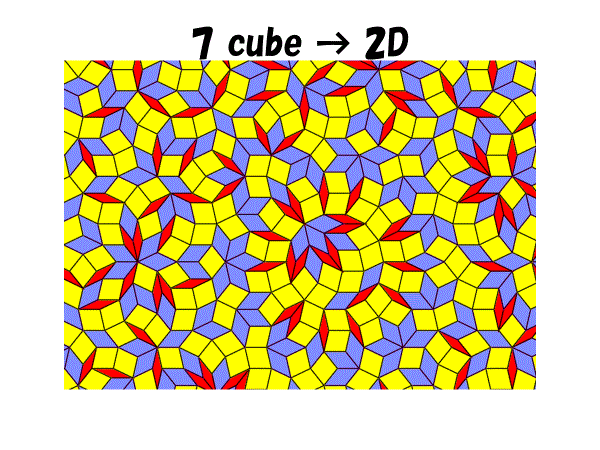
もし７回回転対称にしたければ正十四角形の中心角π／７から導かれた３種類の菱形（π／７−６π／７，２π／７−５π／７，３π／７−４π／７）を使うとよいことがわかる．ペンローズ・タイル貼りに見た目がよく似たものができる．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝