定幅図形

円はどの方向の幅も一定となる．いかなる方向に対しても等しい幅をもっている図形を「定幅図形」と呼ぶ．

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

しかし、平面における定幅図形は円だけではなく，そのような形状は無数にあります．たとえば、・・・

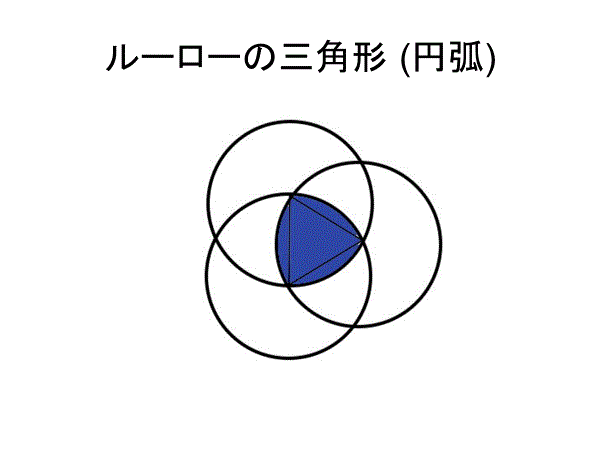
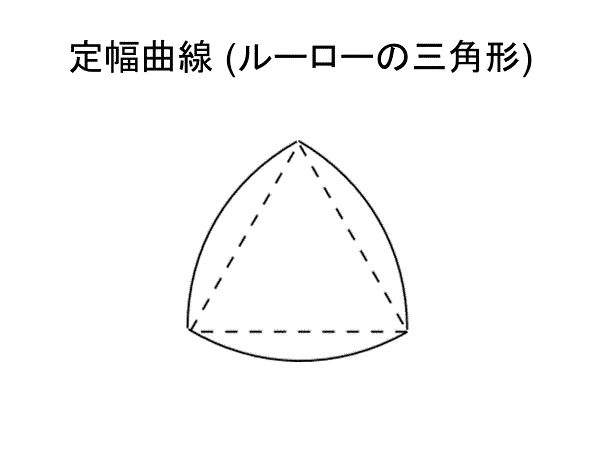
正三角形の３つの頂点を中心にして正三角形の１辺の長さを半径とする円を描くと，正三角形に少し丸みをつけた図形ができる．これがルーローの三角形である．ルーローの三角形はどの方向の幅も最初の正三角形の１辺の長さとなる．

定幅曲線定理

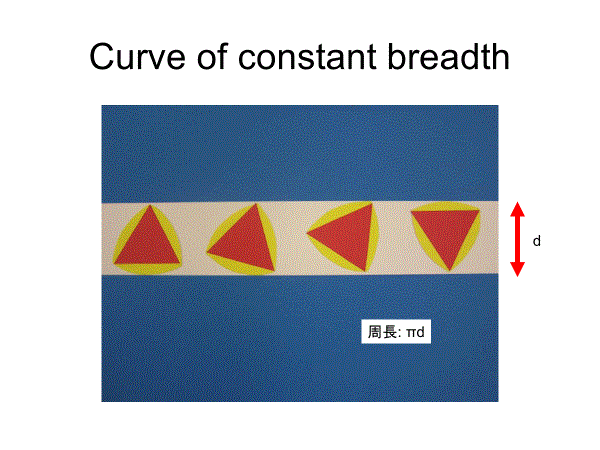
1.幅ｄのすべての定幅曲線の周長はπｄで等しい（バービエ）

2.定幅曲線のなかで面積が最大になるのは円、最小になるのはルーローの三角形である（ブラシュケ、ルベーグ）

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

定幅曲線: ルーローの三角形の平行曲線なども定幅曲線の例です。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝