ルーローの三角形の中心は楕円をつないだ曲線を描く

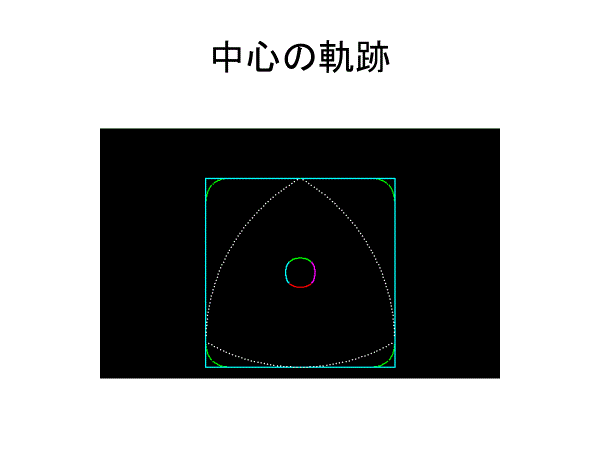
しかし、楕円の区分的連結を実現させることは難しい。工学応用を果たすためには中心軌道が円になる必要があるが、どうしたらよいだろうか？

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

半径の異なる２つの円があり，半径Ｒの円に半径ｒ（＜Ｒ）の円が内接している場合に，半径ｒの円を固定し，半径Ｒの円が半径ｒの円を偏心回転するとき，半径Ｒの円周上の点Ｐの軌跡をペリトロコイドといいます．フラフープ曲線をイメージ擦れがわかりやすいのですが、一般に、正（ｎ−１）角形の頂点を（ｎ−１）公転について１回自転させることによってペリトロコイド曲線を描くことができます。

n=4の場合を考えますが、パラメータを調節することによって、近似的な正方形（あるいはスタジアム型)を描くことが可能です。すなわち、ｎ＝４の場合は自転と公転の向きを変えることによって、２角形と４角形が得られるというわけです。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

これで外枠ができたのですが、引き続き、その内転形を設計する必要があります。

内転形は外枠となるペリトロコイド曲線を（ｎ−２）公転について１回自転（偏心回転）させ、その内包絡線を求めます。ｎ＝４の場合はルーローの三角形に類似した包絡線が得られます。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝