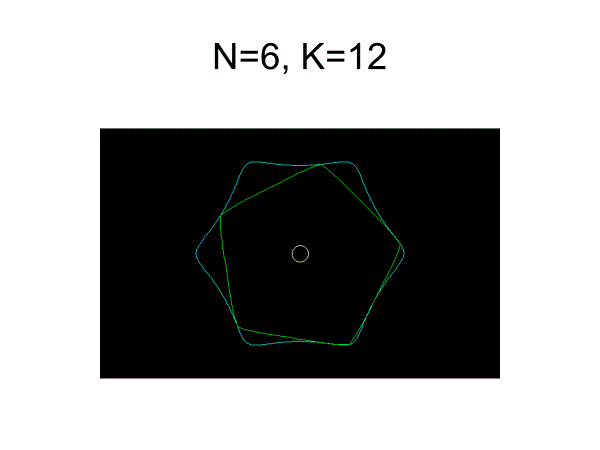
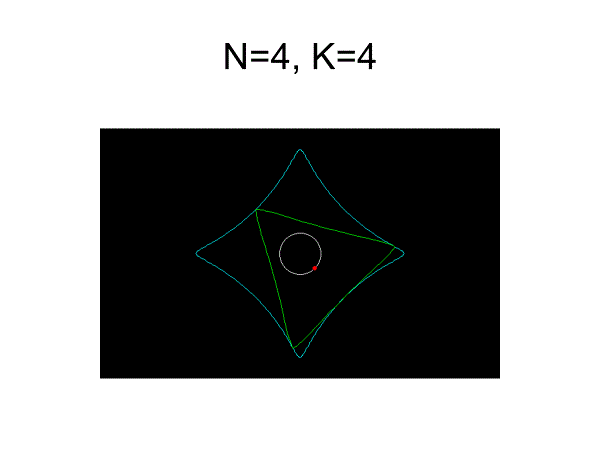
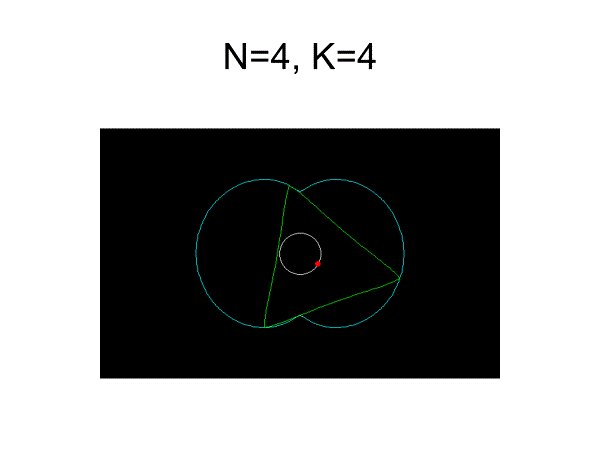
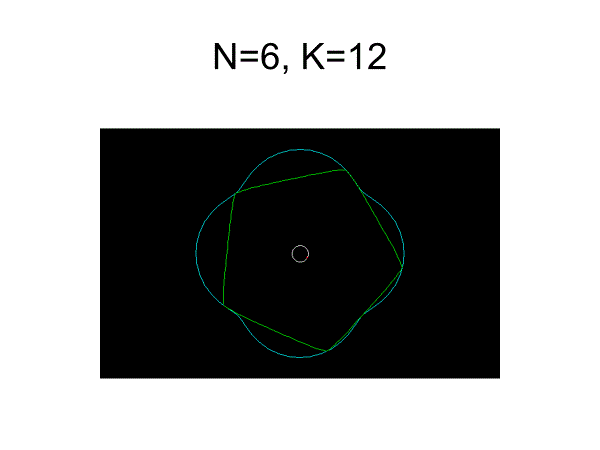
ペリトロコイド曲線

x=e・cos(n-1)t+R・cost

y=e・sin(n-1)t+R・sint

は古代ギリシャ時代から天体の運動模型として使われてきた曲線である。

パラメータを変更するといろいろな曲線が描かれる。K=R/e

これからは美術館だと思っていただき、鑑賞することにしよう。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

ローターが直線で近似できるもの

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

回転方向を逆にしたもの

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝