π/8（デルトイド）より面積の小さい星状領域、できればπ/11より面積の小さい星状領域を構成してみたいのであるが、

実際問題としてデルトイドより面積の小さい星状領域をみつけることは簡単な問題ではない。

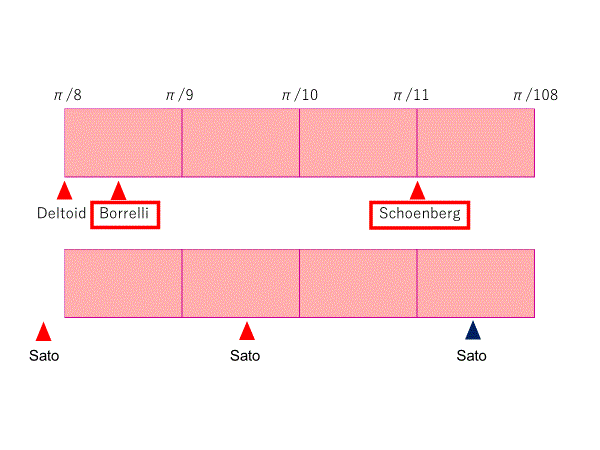
これからはすでに知られているシェーンベルグ集合、ボレリ集合を含む５種類の異なる星状集合を扱う。

Circular arc star shaped set (Schoenberg)

Asteroid arc star shaped set (Borrelli)

Peritrochoid arc star shaped set

Pentagram and N-cusped star shaped set

Slender N-cusped star shaped set

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝

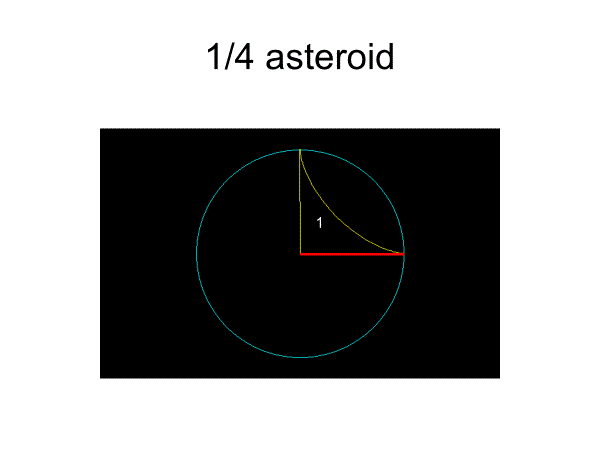
ボレリ集合では、まず1/4アステロイドを考える。

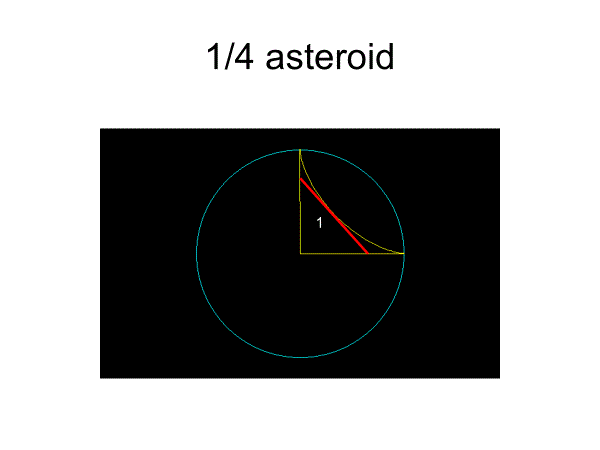
アステロイドは、棒の両端をそれぞれｘ軸・ｙ軸上に置いたまま棒をスライドさせたときの包絡線になっている。

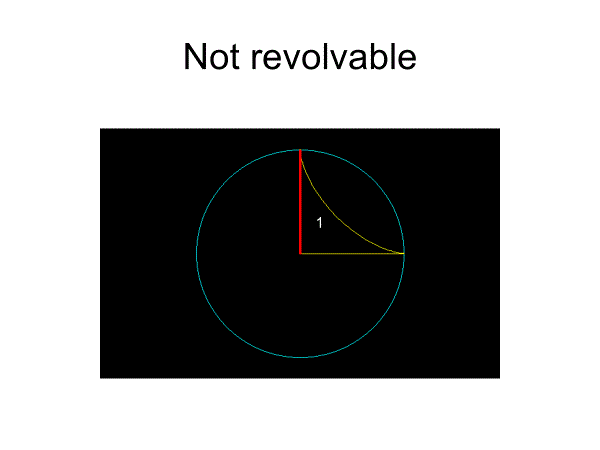
1/4アステロイドは掛谷集合ではないが、これを2個合わせて半アステロイドにすると、棒が１回転することができる掛谷集合となる。

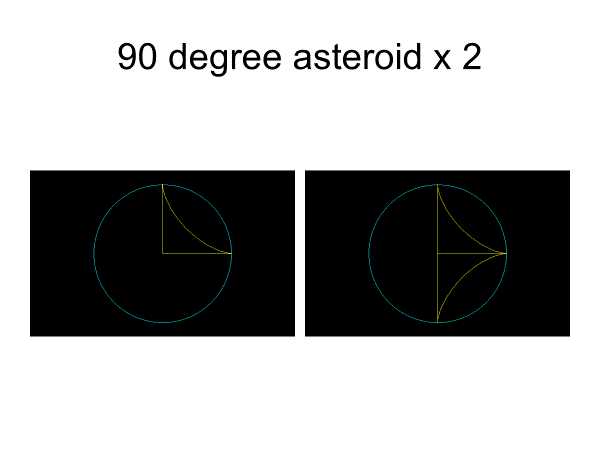
同様に120°アステロイドx3

135°アステロイドx4, 144°アステロイドx5,150°アステロイドx6で掛谷集合を構成することができる。

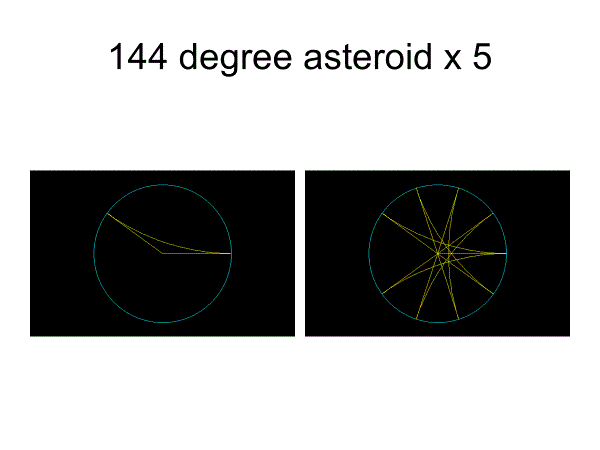
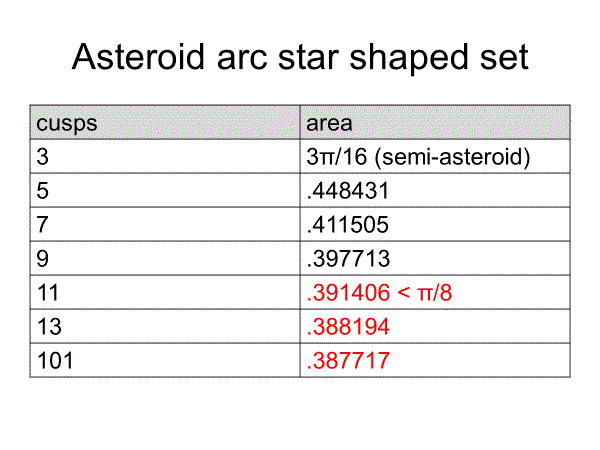
面積は単調に減少するわけではないが、π/8よりは小さくなる。

＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝＝